cos∠(a,b)=(6·(n²-(m+1)²)-5·(m+1)·n)/(4·(m+1)²-9·n²)
Пошаговое объяснение:
Векторов выделим жирным шрифтом.
Скалярное произведение векторов a и b определяется по формуле:
(a, b) = |a|·|b|·cos∠(a,b),
где ∠(a,b) - угол между векторами a и b.
|a|²=(a, a) = ( (m+1)·p+n·q, (m+1)·p+n·q ) =(m+1)²·p²+2·(m+1)·n·(p,q)+n²·q²=
=(m+1)²·|p|²+2·(m+1)·n·(|p|·|q|·cos∠(p,q))+n²·|q|²=
=(m+1)²·2²+2·(m+1)·n·2·3·cos(π/3)+n²·3²=4·(m+1)²+12·(m+1)·n·1/2+9·n²=
=4·(m+1)²+6·(m+1)·n·+9·n²=(2·(m+1)+3·n)²
Тогда |a| = 2·(m+1)+3·n.
|b|²=(b, b) = ( n·p-(m+1)·q, n·p-(m+1)·q ) =n²·p²-2·(m+1)·n·(p,q)+(m+1)²·q²=
=n²·|p|²-2·(m+1)·n·(|p|·|q|·cos∠(p,q))+(m+1)²·|q|²=
=n²·2²-2·(m+1)·n·2·3·cos(π/3)+(m+1)²·3²=4·(m+1)²-12·(m+1)·n·1/2+9·n²=
=4·n²-6·(m+1)·n·+9·(m+1)²=(2·(m+1)-3·n)²
Тогда |b|=2·(m+1)-3·n.
С другой стороны:
(a, b) = ( (m+1)·p+n·q, n·p-(m+1)·q)= (m+1)·n·p²+n²·(q, p)-(m+1)²·(q,p)-(m+1)·n·q²=
=(m+1)·n·|p|²+(n²-(m+1)²)·(|p|·|q|·cos∠(p,q))-(m+1)·n·|q|²=
=(m+1)·n·2²+(n²-(m+1)²)·2·3·cos(π/3)-(m+1)·n·3²=(m+1)·n·(4-9)+(n²-(m+1)²)·6·1/2=
= -5·(m+1)·n+6·(n²-(m+1)²)
Тогда
-5·(m+1)·n+6·(n²-(m+1)²)=(2·(m+1)+3·n)·(2·(m+1)-3·n)·cos∠(a,b)
cos∠(a,b)·(2·(m+1)+3·n)·(2·(m+1)-3·n)= -5·(m+1)·n+6·(n²-(m+1)²)
cos∠(a,b)=(6·(n²-(m+1)²)-5·(m+1)·n)/((2·(m+1)+3·n)·(2·(m+1)-3·n)) или
cos∠(a,b)=(6·(n²-(m+1)²)-5·(m+1)·n)/(4·(m+1)²-9·n²)
45 км/ч скорость, при которой Арлан приедет вовремя
Пошаговое объяснение:
Пусть v - скорость, t - время, при котором Арлан приедет на работу вовремя
Путь до работы S = vt
Переведём 15 мин в часы: 15/60 = 1/4 часа
По условию задания имеем:
S/36 = t + 1/4 - опоздает на 15 минут
S/60 = t - 1/4 - приедет на 15 минут раньше
Исходя из этого имеем:
S = 36(t + 1/4) = 36t + 9
S = 60(t - 1/4) = 60t - 15
36t + 9 = 60t - 15
24t = 24
t = 24 : 24 = 1 (час) - время, при котором Арлан приедет на работу вовремя
S = 36t + 9 = 36*1 + 9 = 45 (км) путь от дома до работы
v = S/t = 45/1 = 45 (км/ч ) скорость, при которой Арлан приедет вовремя
Площадь листа 5*5 = 25 кв.дм.
Площадь круга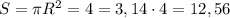
Площадь неиспользованной фанеры 25-12,56 = 12,44 кв.дм.