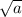Разрешите уравнения , учитывая четность второго коэффициента: 5x^2+26x-24=0

👇

Увидеть ответ

Ответ:

bdoyan1994

27.05.2023

Найдем дискриминант квадратного уравнения:

D = b² - 4ac = 26² - 4·5·(-24) = 676 + 480 = √1156=34

Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:

x1 = (-26 - 34)/2*5= -60/10 = -6

x2 = (-26 + 34)2·5 = 8/10= 0.8

ответ(-6 ; 0,8)

4,4(57 оценок)

Открыть все ответы

Ответ:

olga14081

27.05.2023

Для избавления от иррациональности в знаменателе необходимо вначале проанализировать знаменатель.
Если знаменатель представляет собой выражение вида $\sqrt{a}$ , то необходимо домножить и числитель, и знаменатель на этот корень (основное свойство дроби)
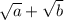Если знаменатель представляет собой выражение вида $\sqrt{a}- \sqrt{b}$ или $\sqrt{a}+ \sqrt{b}$ , то числитель и знаменатель необходимо домножить на сопряжённое выражение (для первого: на 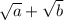$\sqrt{a}+\sqrt{b}$ ; для второго выражения на 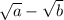$\sqrt{a}-\sqrt{b}$ ), сведя числитель к формуле разности квадратов. Это алгоритм для квадратных корней. Для корней больше 2 степени сопряжённые ищутся иначе и по другим формулам.

4,6(27 оценок)

Ответ:

alisa0901

27.05.2023

Плавание – самый красивый , и самый полезный вид спорта. Оно имеет необычайно давнюю историю. Ещё Древними славянами проводились соревнования по плаванию, суть их была такова: люди плавали в реке и ловили рыбу руками, тот кто приносил на берег самую крупную рыбу, того и считали победителем. Эти соревнования совсем не похожи на современные, но тем не менее, умение плавать имело в них решающее значение. Плавание не мало важно для здоровья человека, т.к во время занятии этим видом спорта очищается кровь , развивается дыхательная система, а также при занятиями плаванием кровь насыщается кислородом. Так же этот вид спорта снимает психологическую нагрузку. В воде нервная система успокаивается. При нахождении человека в воде снимается напряжение в области позвоночника и тазобедренного сустава, и именно поэтому оздоровительное плавание обширно используется в медицине. В XX веке люди стали сочетать такие дисциплины как плавание и аэробика – аквааэробика. Этим методом плавания пользуются в основном люди с повышенным весом , проблемами спины.
.История плавания до н.э.

Со времени своего появления на Земле человек всегда был связан с водой. Именно в долинах больших рек - Нила, Тигра и Евфрата, Хуанхе и Янцзы, Инда и Ганга - зародилась человеческая цивилизация. Вода имела огромное значение в жизни первобытных людей, что послужило причиной обожествления этой стихии, внушавшей слабому еще в борьбе с природой человеку чувство преклонения и страха. Культ воды существовал практически у всех народов с самых древних времен.
В 1890 г. впервые проходит первенство Европы по плаванию, в 1896 г. его включают в программу первых современных Олимпийских игр. Особую популярность плавание приобрело в конце 19 века. В 1890 было проведено первое первенство Европы по плаванию. В 1894 году соревнования по плаванию были включены в программу современных Олимпийских игр, что оказало большое влияние на развитие всех видов плавания.

4,4(89 оценок)

Это интересно:

Семейная-жизнь

18.02.2023

Как придумать крутое и запоминающееся прозвище для себя или других?...

Образование-и-коммуникации

26.01.2022

Как хорошо учиться: советы, методы и секреты...

Компьютеры-и-электроника

03.08.2020

Вредоносное ПО в Facebook: как избавиться от него...

Кулинария-и-гостеприимство