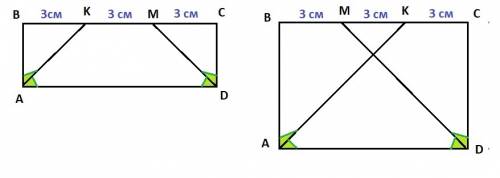
Задача имеет два решения.
1) Прямоугольник ABCD : AK и DM - биссектрисы; BK = KM = MC = 3 см
∠BAK = ∠DAK = 90° / 2 = 45° - AK - биссектриса
∠BKA = ∠DAK = 45° - накрест лежащие углы при AD║BC и секущей AK
ΔABK - прямоугольный равнобедренный : ∠B = 90°; ∠BAK = ∠BKA = 45° ⇒
AB = BK = 3 см
BC = BK + KM + MC = 3 + 3 + 3 = 9 см
Периметр прямоугольника ABCD :
P = (AB + BC) · 2 = (3 + 9) · 2 = 24 см
P = 24 см
================================
2) Прямоугольник ABCD : AK и DM - биссектрисы; BM = MK = KC = 3 см
∠BAK = ∠DAK = 90° / 2 = 45° - AK - биссектриса
∠BKA = ∠DAK = 45° - накрест лежащие углы при AD║BC и секущей AK
ΔABK - прямоугольный равнобедренный : ∠B = 90°; ∠BAK = ∠BKA = 45° ⇒
AB = BK = BM + MK = 3 + 3 = 6 см
BC = BM + MK + KC = 3 + 3 + 3 = 9 см
Периметр прямоугольника ABCD :
P = (AB + BC) · 2 = (6 + 9) · 2 = 30 см
P = 30 см
Задача имеет два решения.
1) Прямоугольник ABCD : AK и DM - биссектрисы; BK = KM = MC = 3 см
∠BAK = ∠DAK = 90° / 2 = 45° - AK - биссектриса
∠BKA = ∠DAK = 45° - накрест лежащие углы при AD║BC и секущей AK
ΔABK - прямоугольный равнобедренный : ∠B = 90°; ∠BAK = ∠BKA = 45° ⇒
AB = BK = 3 см
BC = BK + KM + MC = 3 + 3 + 3 = 9 см
Периметр прямоугольника ABCD :
P = (AB + BC) · 2 = (3 + 9) · 2 = 24 см
P = 24 см
================================
2) Прямоугольник ABCD : AK и DM - биссектрисы; BM = MK = KC = 3 см
∠BAK = ∠DAK = 90° / 2 = 45° - AK - биссектриса
∠BKA = ∠DAK = 45° - накрест лежащие углы при AD║BC и секущей AK
ΔABK - прямоугольный равнобедренный : ∠B = 90°; ∠BAK = ∠BKA = 45° ⇒
AB = BK = BM + MK = 3 + 3 = 6 см
BC = BM + MK + KC = 3 + 3 + 3 = 9 см
Периметр прямоугольника ABCD :
P = (AB + BC) · 2 = (6 + 9) · 2 = 30 см
P = 30 см

Рассмотрим отдельно каждое из слагаемых.
4sinx, 24/pi x, 26
4sinx - периодическая функция, которая на [-5pi/6, -pi/2] убывает и достигает своего минимального значения -1, и на [-pi/2, 0] возрастает и достигает своего максимального значения 0.
24/pi x - возрастающая функция => наибольшее значение она примет в 0.
26 - постоянная, не меняющаяся на этом интервале.
Таким образом, функция может принять свое наименьшее значение в точке -5pi/6 или -pi/2.
y(-pi/2) = -4 - 12 + 26 = 10
y(-5pi/6) = - 2 - 20 + 26 = 4
min = 4 на этом промежутке