1)
а)0,98 противоположное -0,98
б)981 противоположное -981
в) -23 противоположное 23
г) -2,7 противоположное 2,7
2)
а) -19,6 ÷ (-0,4) = 49;
б) -18-16 = -34;
в) -56+34 = -22;
г) 5,7*(-0,3) = -1,71
3)
а) -699+42-276+699+276= 42
1) -699+699 = 0;
2) -276+276 = 0;
3) 0+0+42 = 42.
б) 5,7-27-53-5,7+2,5= -77,5
1) 5,7-5,7=0;
2) -27-53 = -80;
3) -80+2,5 = -77,5.
в) 212-29,5-212+891+29,5 = 891
1) 212-212 = 0;
2) 29,5-29,5 = 0;
3)0+0+891 = 891.
4)
а) 33,5(х-29) = 0
33,5х-971,5 = 0
33,5х=971,5
х = 971,5 ÷ 33,5
х = 29.
б) (х+13)*7 = 0
7х+91 = 0
7х= -91
х = -91÷7
х= -13.
в) (х-2)(х+15)=0
х-2 = 0 або х+15 = 0
х = 2 х= -15
№ 4. x ≤ 0.75
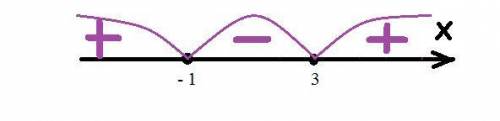
№ 5. ( - ∞; - 1 ] ∪ [ 3; + ∞ )
Пошаговое объяснение:
№ 4. 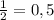
Тогда выражение имеет вид:
(0,5)^ (2*x) ≥ (0.125) ^ (1/2)
(0.5) ^ (2*x) ≥ ((0.5)^3)^(1/2)
(0.5) ^ (2*x) ≥ (0.5) ^ (3*(1/2)
(0.5) ^ (2*x) ≥ (0.5) ^ (3/2)
(0.5) ^ (2*x) ≥ (0.5) ^ 1.5
Т.к. 0,5 < 1, то имеем:
2 * х ≤ 1.5
x ≤ 1.5 / 2
x ≤ 0.75 или иначе записать можно так х ≤ 
№ 5. 7 ^ (x ^ 2) * 49 ^ ( - x) ≥ 343
7 ^ (x ^ 2) * 7^2^ ( - x) ≥ 7 ^ 3
7 ^ (x ^ 2) * 7^ ( - 2 * x) ≥ 7 ^ 3
7 ^ ((x ^ 2) + ( - 2 * x)) ≥ 7 ^ 3
7 ^ (x ^ 2 - 2 * x) ≥ 7 ^ 3
Т.к. 7 > 1, то запишем так:
x ^ 2 - 2 * x ≥ 3
Решим получившееся квадратное неравенство.
x ^ 2 - 2 * x = 3
x ^ 2 - 2 * x - 3 = 0
D = 16
x1,2 = (2±4)/2
x1 = 3 и x2 = -1
Решим методом интервалов.
( - ∞; - 1 ] ∪ [ 3; + ∞ )
8х×8х-64х=+1-1+1-2
0х=-1
Решений нет