Пошаговое объяснение:
Проведем из вершины В параллелограмма высоты ВК и ВН к сторонам АД и СД.
Так как у параллелограмма длины противоположных сторон равны, то АД = ВС = 18 см, СД = АВ = 12 см.
Применим формулу площади параллелограмма.
S = АД * ВК и S = СД * ВН.
S = 18 * ВК = 144.
ВК = 144 / 18 = 8 см.
Из прямоугольного треугольника МВК, по теореме Пифагора, определим длину гипотенузы МК.
МК2 = ВК2 + МВ2 = 82 + 122 = 64 + 144 = 208.
МК = 4 * √13 см.
S = СД * ВН.
S = 12 * ВН = 144.
ВК = 144 / 12 = 12 см.
Из прямоугольного треугольника МВН, по теореме Пифагора, определим длину гипотенузы МН.
МН2 = ВН2 + МВ2 = 122 + 122 = 144 + 144 = 228.
МН = 2 * √12 см.
ответ: Расстояния от точки M до прямой AД равно 4 * √13 см, до прямой CД равно 2 * √12 см.
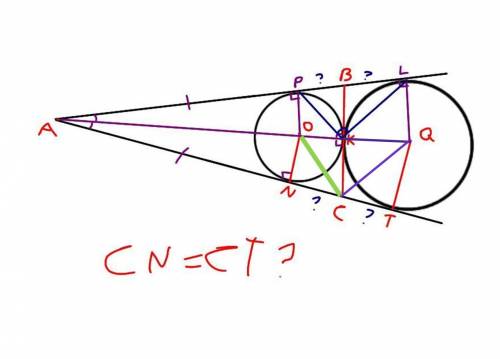
1) Рассмотрим ΔONC и ΔOKC.
У них:
∠ONC= ∠OKC=90°
ON=OK=r (радиусы одной окружности)
сторона OC-общая
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны.
Из равенства треугольников следует равенство соответственных сторон.
ΔONC = ΔOKC => CN=KC
2) Рассмотрим ΔQKC и ΔQTC (рассуждаем аналогично)
У них
∠QKC= ∠QTC=90°
ON=OK=R (радиусы одной окружности)
QC-общая
ΔQKC = ΔQTC => КС=CT
3) Если CN=KC, а KC = CT, то => CN=CT Если каждая из двух данных сторон равна третьей, то эти стороны равны между собой (свойство транзитивности).
Доказано.
Значит в данном задании таких 2 дроби: 6,1333... и 8,(7)
то есть 6,1(3) и 8,(7). Такие дроби называются периодическими