1) 1л:20=1/20 -1 час 1 труба
2) 1л:30=1/30-1 час 2 труба
3) 1/20+1/30=5/60=1/12 всего
4) 1/12:1=12ч две трубы
1. Where do you and your family go in the summer?
2. Where do your best friend live?
3. Whe do you do sport?
4. How do you go to school?
5. What films do your friends like?
6. Who do you help in your family?
7. What do you do in the evening?
Сначала рассмотрим вопрос с временами Simple. Для примера возьмем вопросительное слово what – что.В настоящем времени порядок слов в вопросе следующий:
What + do \ does + подлежащее + verb?
Примеры:
What do they like? – Что им нравится?
What does she read? – Что она читает?
What do you do? – Чем вы занимаетесь?
Также вместо "What", может быть
• What – что,
• Who – кто,
• Where – где,
• Why – почему,
• When – когда,
• Whose – чей,
• Which – какой, который
• How – как
Также в ход могут идти вопросительные словосочетания с участием этих слов, например: how long – как долго, what time – в какое время, what colour – какого цвета и др.
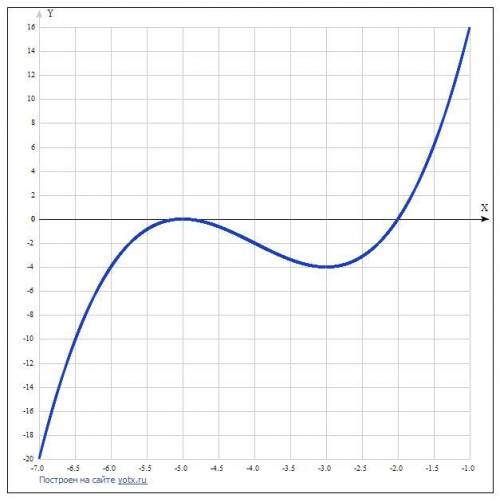
Дана функция y=x³ +12x²+45x+50.
1. Определить область определения функции:
ограничений нет, вся числовая ось: D(f) = R.
2. Исследовать функцию на четность не четность:
f(-x) = (-x)³ + 12(-x)² + 45(-x) + 50 = -x³ + 12x²- 45x + 50 ≠ f(x),
f(-x) = -(x³ - 12x²+ 45x - 50) ≠ f(x). Значит, функция общего вида.
3. Найти координаты точек пересечения графика функции с осями координат:
- с осью Оу при х = 0. у = 50.
- с осью Ох при у = 0.
Надо решить уравнение x³ + 12x²+ 45x + 50 = 0.
Находим корни этого уравнения среди множителей свободного члена.
50 = +-1*+-2*+-5*+-5.
При подстановке определяем: х = -2 и х = -5 (2 раза).
x³ + 12x²+ 45x + 50 = (х + 2)*(х + 5)*(х + 5) = 0. х = -2 и х = -5.
4. Исследовать функцию на непрерывность, определить характер точек разрыва функции, если они имеются; найти асимптоты кривой:
точек разрыва и асимптот функция не имеет.
5. Найти интервалы возрастания и убывания функции и ее экстремумы.
Производная равна 3x²+ 24x + 45 = 3(x²+ 8x + 15).
Приравниваем её нулю (множитель в скобках):
x²+ 8x + 15 = 0.
Д = 64 - 4*1*15 = 4. х = (-8 +- 2)/2 = -3 и -5.
Находим знаки производной на полученных промежутках.
х = -6 -5 -4 -3 -1
y' = 9 0 -3 0 24.
Переход с + на - это максимум (х = -5, у = 0), с - на + это минимум(х = -3, у = -4). На промежутке (-∞; -5) и (-3; +∞) функция возрастает, на промежутке (-5; -3) функция убывает.
6. Найти интервалы выпуклости вверх и выпуклости вниз; определить точки перегиба
: y'' = (3x²+ 24x + 45)' = 6x + 24 = 6(x + 4) = 0.
Точка перегиба х = -4, у = -2.
Находим знаки второй производной на полученных промежутках.
x = -5 -4 -3
y'' = -6 0 6.
Где вторая производная меньше нуля, там график функции выпуклый, а где больше - вогнутый:
• Выпуклая на промежутке: (-∞; -4).
• Вогнутая на промежутке: (-4; +∞).
7. Построить график функции.
Таблица точек:
x y
-7.0 -20
-6.5 -10.1
-6.0 -4
-5.5 -0.9
-5.0 0
-4.5 -0.6
-4.0 -2
-3.5 -3.4
-3.0 -4
-2.5 -3.1
-2.0 0
-1.5 6.1
-1.0 16
График - в приложении.
 1. определить область существ" />
1. определить область существ" />
Наверное, спрашивается: за сколько часов они вместе наполнят бассейн.
1/20 + 1/30 = (3+2)/60 = 5/60 = 1/12
За 12 часов.