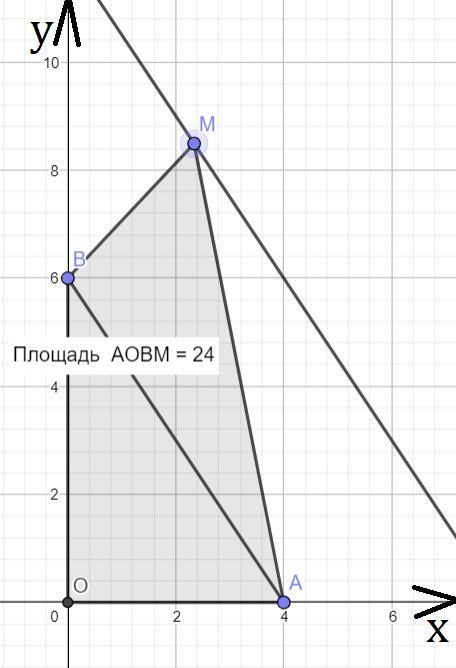
Прямая проходящая через точки A, B имеет уравнение:
y=ax+t, подставим координаты точек чтобы найти уравнение в явном виде.
6=a·o+t ⇒ t=6; 0=a·4+t ⇒ a=-6/4=-1,5
y = -1,5x+6
Исходя из последовательности вершин четырёхугольника, получаем, что координаты M(x;y) удовлетворяют неравенству y≥-1,5x+6.
Заметим, что S(AOBM) = S(AOB)+S(BMA), при этом S(AOBM)=24, S(AOB)=AO·OB/2=12.
Тогда S(BMA)=12.
Поскольку площадь треугольника постоянная и длина стороны AB тоже. То высота опущенная из M на AB должна быть постоянной, откуда M лежит на прямой параллельной AB. Тогда угол наклона k равен углу наклона прямой проходящей через точки A, B.
k = -1,5
ответ: -1,5.
Правильный ответ — Г.
Пошаговое объяснение:
Используя второе условие, мы можем сразу узнать площадь треугольника, благодаря значению высоты, которое нам дано по условию.
S = 1/2 AC × AH (AC - основание, AH - высота);
S = 1/2 6 × 4;
S = 3 × 4;
S = 12.
При использовании первого условия необходимо узнать значение основания. Так как у нас проведена высота, мы имеем два прямоугольных треугольника. Рассмотрим из них ∆ABH, в котором известна гипотенуза AB и высота AH. Через теорему Пифагора (c² = a²+b²) можно узнать значение катета BH.
5² = a²+4²;
a² = 5² - 4²;
a = √5² - 4²;
a = √25 - 16;
a = √9;
a = 3.
К слову, прямоугольные треугольники ∆ABH и ∆ACH являются египетскими (треугольник, у которого катеты равны 3 и 4, а гипотенуза – 5).