1) 
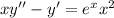
Поскольку x = 0 не является решением данного дифференциального уравнения, то поделим обе части уравнения на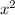 
, получаем
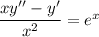
В левой части уравнения это ни что иное как формула производной частного, то есть :
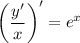
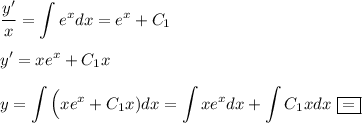
Подсчитаем отдельный интеграл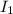 
по частям.
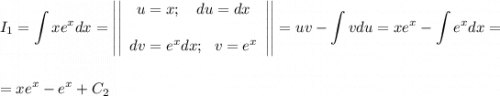
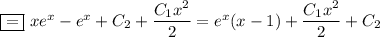
2) 
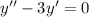
Это линейное однородное дифференциальное с постоянными коэффициентами. Замена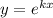 
, перейдём к характеристическому уравнению: 
, 
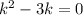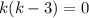корни которого 
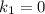и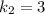 
. Тогда общее решение диф. уравнения: 
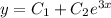и его первая производная 
.
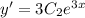Осталось найти константы C₁ и C₂ , подставляя начальные условия.
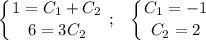
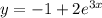— частное решение.
Пошаговое объяснение:
1. Выразим b через x:
{2x^2 + (3b - 1)x - 3 = 0;
{6x^2 - (2b - 3)x - 1 = 0;
{(3b - 1)x = 3 - 2x^2;
{(2b - 3)x = 6x^2 - 1;
{3b - 1 = (3 - 2x^2)/x;
{2b - 3 = (6x^2 - 1)/x;
{3b = (3 - 2x^2)/x + 1;
{2b = (6x^2 - 1)/x + 3;
{6b = 2(3 - 2x^2)/x + 2;
{6b = 3(6x^2 - 1)/x + 9.
2. Приравняем правые части уравнений:
2(3 - 2x^2)/x + 2 = 3(6x^2 - 1)/x + 9;
2(3 - 2x^2) + 2x = 3(6x^2 - 1) + 9x;
6 - 4x^2 = 18x^2 - 3 + 7x;
22x^2 + 7x - 9 = 0;
D = 7^2 + 4 * 22 * 9 = 49 + 792 = 841 = 29^2;
x = (-7 ± 29)/44;
1) x1 = (-7 - 29)/44 = -36/44 = -9/11;
b = ((6x^2 - 1)/x + 3)/2;
b = 3x - 1/2x + 3/2 = -27/11 + 11/18 + 3/2 = (-486 + 121 + 297)/198 = -68/198 = -34/99 (не целое число);
2) x2 = (-7 + 29)/44 = 22/44 = 1/2;
b = 3x - 1/2x + 3/2 = 3/2 - 1 + 3/2 = 2 (целое число).
ответ: 2.
9