Пошаговое объяснение:
1) 900:4=225(м) - длина одной стороны квадрата.
2)225×4=900(м)
ответ: периметр квадрата равен 900 метрам.
Для проверки можно составить обратную задачу, в которой нужно узнать площадь, зная длину стороны одного квадрата.
Длина одной стороны квадрата равна 225 м. Вычислите площадь этого квадрата.
225×4=900(м)
ответ: площадь этого квадрата равна 900 м². Если данные, которые мы узнали совпадают с данными обратной задачи, значит задача решена верно.
Если так и запишешь, то оценку явно повысят. Поверь, я очень старалась, я не искала в интернете и у меня нет такой задачи в учебнике. Думаю, я заслужила 5 звёзд и
1. Область определения функции - ограничений нет, х ∈ Z.
2. Точки пересечения функции с осями координат.
С осью Оу при х = 0, у = -5.
С осью Ох при у = 0. Надо решить такое уравнение: -х³ + 3х - 5 = 0.
Для вычисления корней кубического уравнения используются формулы Кардано.
Для начала уравнение приводится к виду:
y³ + py + q = 0. ответ: 1 точка х = -2,279.
4. Производная равна: y' = -3х +3
5. 6. Промежутки возрастания, убывания, экстремумы функции.
Приравниваем производную нулю: -3х² + 3 = -3(х² - 1) = 0.
Отсюда имеем 2 критические точки: х = 1 и х = -1.
Находим знаки производной на полученных промежутках:
х = -2 -1 0 1 2
y' = -9 0 3 0 -9.
Минимум в точке х = -1, у = -7 (переход с - на +),
максимум в точке х = 1, у = -3 (переход с + на -).
Функция возрастает при y' > 0, это промежуток (-1; 1).
Убывает (-∞; -1) ∪ (1; +∞).
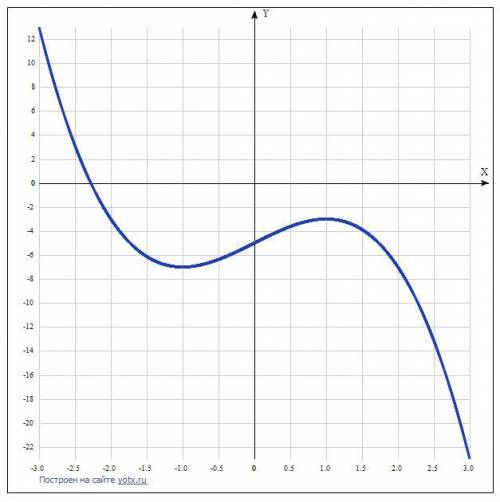
7. Построение графика.
Таблица точек:
x y
-3.0 13
-2.5 3.1
-2.0 -3
-1.5 -6.1
-1.0 -7
-0.5 -6.4
0 -5
0.5 -3.6
1.0 -3
1.5 -3.9
2.0 -7
2.5 -13.1
3.0 -23.
Попробуем найти фальшивый изумруд из 13, зная, что он легче настоящего.
Делим на 3, 3, 7.
1 взв.) Сравниваем две кучки по 3. Если одна легче, то в ней фальшивка.
2 взв.) Сравниваем 2 изумруда из фальшивой кучки, находим фальшивый. Если они равны, то фальшивый третий.
1 взв.) Если кучки изумрудов по 3 одинаковые, то делим 7 на 3, 3, 1
2 взв.) Опять сравниваем две по 3 с тем же результатом.
Если кучки опять равны, то
3 взв.) Сравниваем любой изумруд с 1 отложенным.
Если и 3-ий раз будет равенство, то фальшивый сапфир, а не изумруд.
На сапфиры нужно еще 3 взвешивания. Действуем точно также.
Делим 14 сапфиров на 3, 3, 8
1 взв.) Сравниваем две кучки по 3. Если одна тяжелее, фальшивка в ней.
2 взв.) Сравниваем два сапфира, находим фальшивый тяжелый.
Если они равны, то фальшивый - третий.
1взв.) Если две кучки по 3 равны, то берем 8, делим на 3, 3, 2.
2 взв.) Опять сравниваем две по 3, находим тяжелую, фальшивка в ней.
3 взв.) Находим фальшивку.
2 взв.) Если две новые кучки по 3 равны, то
3 взв. ) Берем один камень из 2 и сравниваем с любым нормальным.
Если он тяжелее, то он фальшивый.
Если они равны, то фальшивый - оставшийся из 2, который не проверяли.
Всего 6 взвешиваний.
Замечу, что если бы было 27 одинаковых камней, и неизвестно, тяжелее или легче фальшивый камень, то 6 взвешиваниями не обойтись.
Странно, что такого ответа нет в вариантах.