S(ABCD) = 13
Пошаговое объяснение:
Определим вид четырехугольника.
Найдем длины его сторон:
AB =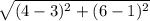 
= 
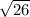
BC =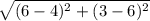 
= 
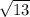
CD =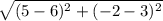 
=
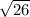
DA =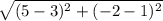 
=
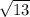
(используется формула расстояния между двумя точками)
У четырехугольника две пары равных сторон, значит, это параллелограмм(по признаку параллелограмма)
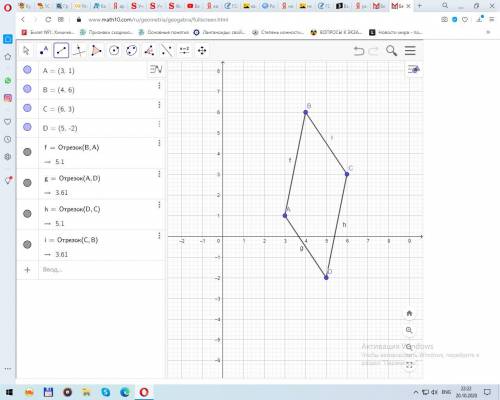
Для наглядности изобразим параллелограмм ABCD на координатной плоскости.
Площадь параллелограмма можно посчитать через сторону и высоту, проведенную к этой стороне:
S(ABCD) = h*a
Примем AB = a, тогда осталось найти высоту, проведенную к стороне AB. Эта высота равна расстоянию от точки C до прямой AB. Значит, можно посчитать высоту, используя формулу расстояния от точки до прямой.
Задаем уравнение прямой AB по двум точкам:
= 
= 
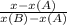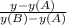
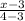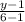
5x - 15 = y - 1
y = 5x - 14 - получили уравнение прямой AB
Запишем уравнение в виде Ax + By + C = 0
5x - y - 14 = 0 (то есть A = 5, B = -1, C = -14)
С(x₀; y₀) = C(6;3) , x₀ = 6, y₀ = 3
h =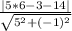 
= 13/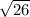
S(ABCD) = 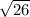* (13/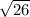) = 13
2)(2,6+1 2/5)×(4-2 4/25)=(2,6+1,4)×(4-2,16)=4×1,84=7,36
3)(7 2/5+6,4)÷(5,2-2 9/10)=(7,4+6,4)÷(5,2-2,9)=13,8÷2,3=6
4)(14-2 3/10)÷(3/5+0,7)=(14-2,3)÷(0,6+0,7)=11,7÷1,3=9