Пошаговое объяснение:
1. S = п*R^2
S = 3,14 * 2^2 =4п= 3,14 * 4 = 12,56 (cм^2)
2.S сектора=(п*R^2 *на угол)/360° ;
S=(п*6^2*60)/360=6п=6*3,14=18,84 (cм^2)
3.C=2πr
S=πr²=4π⇒r==2 (см
)
C=2*2π=4π=12,56 (см)
4.C=2πr=πd;
С=3,14*2=6,28 (см)
5.Длина дуги окружности: πr*n/180, где n - градусная мера дуги.
π*15*60/180=5π =5*3,14=15,7 (см)
6.длина дуги=альфа*r;
2п=альфа*12
альфа=2п:12=п:6=30 градусов
7.Диагональ квадрата больше его стороны в √2 раз. Значит, длина стороны квадрата равна 2. Диаметр вписанной в квадрат окружности равен его стороне, то есть d=2. По формуле длины окружности, l=2πr=πd ⇒ l=2π=2*3,14=6,28 (см)
ДАНО
Y = (x² + 9)/x
ИССЛЕДОВАНИЕ
1. Область определения. Деление на ноль в знаменателе.
Х≠ 1.
Х∈(-∞;0)∪(0;+∞)
2. Вертикальная асимптота: Х= 1.
3. Пересечение с осью Х. Y(x) = 0 - нет.
4. Пересечение с осью У - нет
5. Наклонная асимптота
k = lim(+∞)Y(x)/x = 4*x/x = 4. Уравнение асимптоты: Y = 4*x.
6. Проверка на чётность.
Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x)
Функция ни четная ни нечетная.
7. Поведение в точке разрыва.
lim(->0-) Y(x) = -∞.
lim(->0+) Y(x) = +∞
8, Первая производная.
6. Локальные экстремумы.
Y'(x) = 0, x1 = - 3/2, x2 = 3/2
Максимум Y(-3/2)= .-12.
Минимум Y(3/2) = 12.
7. Участки монотонности функции.
Возрастает - Х∈(-∞;-3/2]∪[3/2;+∞).
Убывает - Х∈[-3/2;0)∪(0;3/2]
8. Вторая производная.
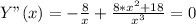
Корней нет. Точек перегиба (на графике) - нет.
9. Выпуклая - "горка" - Х∈(-∞;0). Вогнутая - "ложка" - Х∈(0;+∞)
10. График в приложении

6•1
Но лучше вот так
30:5•1