Пошаговое объяснение:
Метод математической индукции состоит из 2ух шагов.
1)Утверждение P(n) справедливо при n=1. (База индукции)
2)Для ∀k∈N из справедливости P(k) следует справедливость P(k+1)(индуктивный переход)
[a]
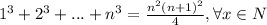
1 шаг: база индукции
Проверяем справедливость при n=1
1³+2³+...+n³=1
(1/4)*1²*(1+1)²=(1/4)*4=1
Верно
2 шаг: Индуктивный переход
Допустим равенство верно для n=k:
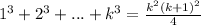
Докажем что формула равна и для n=k+1
(на месте k в формуле должно оказаться k+1)

Доказано
[b]

1 шаг: база индукции
Проверяем справедливость при n=1
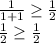
Верно
2 шаг: Индуктивный переход
Допустим равенство верно для n=k:
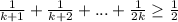
Докажем что формула равна и для n=k+1:


Выражение без скобок ≥1/2, выражение в скобках >0, значит выражение выполняется для k+1
Доказано
коэффициент 4) 126 5)-6 6) -1
Пошаговое объяснение
здесь не РАЗНОСТЬ,а ПРОИЗВЕДЕНИЕ.
4)-7a*3b*(-6c)= 126abc (минус на минус дает плюс -при умножении и при делении)
5)16x*(- 8\15b)* 45\64 k= - 6 x b k
6) -0,2 t*(-5a)*(-b)= - abt
"-" * "-" = "+" это два минуса дадут плюс
а "+" * "-"= "-" плюс на минус дадут минус
если количество минусов четное(2;4;6;8;10) то в произведении или в частном будет "плюс"
если количество минусов нечетное(1;3;5;7; 9) то в произведении или в частном будет "минус"