Уравнение
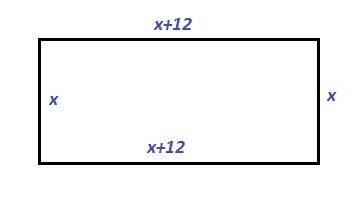
Пусть одна сторона прямоугольника равна х см.
Тогда вторая сторона равна х+12 см.
Периметр прямоугольника
Р = (x + x + 12) · 2 = 4x + 24
По условию периметр равен 1 м = 100 см.
4x + 24 = 100; 4x = 76; x = 19 см; x+12 = 19 + 12 = 31 см.
ответ: 19 см, 31 см.
=========================================
Стороны прямоугольника попарно равны. Периметр прямоугольника равен 1 м = 100 см. Тогда полупериметр прямоугольника (сумма двух не равных сторон) равна 100 : 2 = 50 см.
Известна сумма двух не равных сторон (50 см) и разность двух не равных сторон (12 см по условию).
По правилу решения задач на сумму и разность двух величин :
(50 - 12) : 2 = 19 см - меньшая сторона прямоугольника
19 + 12 = 31 см - большая сторона прямоугольника.
ответ: 19 см, 31 см.
Пошаговое объяснение:
1.
1) 2 5/9 - 1 20/21 = 2 35/63 - 1 60/63 = 1 98/63 - 1 60/63 = 38/63
2) 38/63 : 1 8/49 = 38/63 : 57/49 = 38/63 * 49/57 =
2/9 * 7/3 = 14/27
3) 1 8/9 : 6 = 17/9 * 1/6 = 17/54
4) 14/27 + 17/54 = 28/54 + 17/54 = 45/54 = 5/6
2.
1) 1 17/18 * 1 13/14 = 35/18 * 27/14 = 5/2 * 3/2 = 15/4
2) 2 5/8 : 1 19/20 = 21/8 : 39/20 = 21/8 * 20/39 = 7/2 * 5/13 = 35/26
3) 15/4 - 35/26 = 195/52 - 70/52 = 125/52
4) 2 25/78 - 1 1/26 = 2 25/78 - 1 3/78 = 1 22/78 = 1 11/39
5) 125/52 : 1 11/39 = 125/52 : 50/39 = 125/52 * 39/50 = 5/4 * 3/2 = 15/8 = 1 7/8
1) 28ц 1/10 + 2ц 3/10 = 28,1 + 2,3 = 30,4 (км/ч) - скорость лодки по течению
2) 28ц 1/10 - 2ц 3/10 = 28,1 - 2,3 = 25,8 (км/ч) - скорость лодки против течения
3) 30,4 * 1 = 30,4 (км) - проплывет лодка за 1 час по течению
4) 25,8 * 1 = 25,8 (км) - проплывет лодка за 1 час против течения
ответ: 30,4 км, 25,8 км.