
Відповідь:
1) 10•10 = 100 плиток образовали бы квадрат, если бы плиток хватило. Поскольку их не хватило, то плиток меньше 100.
2) В неполном ряду плиток при раскладывании по 8 не может быть 8 (это уже полный ряд), а в неполном ряду плиток при раскладывании по 9 не может быть 0 плиток (это значит, что нет неполного ряда), а это означает, что в неполном ряду плиток при раскладывании по 8 плиток может быть только 7, а в неполном ряду плиток при раскладывании по 9 может быть только 1 плитка. Разница как раз составляет 6 плиток, как указано в условии.
3) Представим себе, что есть n полных рядов плиток при раскладывании их по 8, и есть 7 плиток в неполном ряду. Можно перекладывать из неполного ряда по одной плитке к каждому ряду, так, что в каждом ряду образуется по 9 плиток. Так можно делать до тех пор, пока в неполном ряду не останется 1 плитка:
Получаем уравнение
8n + 7 = 9n + 1
9n - 8n = 7 - 1
n = 6 рядов по 8 или по 9 плиток.
4) 8n+7 = 8•6+7=47+7=55 плиток.
Или
9n+1 = 9•6+1=54+1=55 плиток.
ответ: 55 плиток.
Покрокове пояснення:
Дано
Площадь одной плитки = 400:
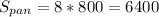
Найти к-во Q потребующихся для замощения панели плиток
Решение
Нужно разделить пл. всей панели на пл. 1 плитки:
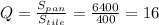
ответ 16
Задача 2Дано
Периметр прямоугольника (Prec) = 120. У прямоугольника противоположные стороны равны. Сторона a = b + 10 Сторона b = x (тогда a = x + 10)Найти площадь прямоугольника Srec
Решение
Исходя из формулы нахождения P прямоугольника, имеем
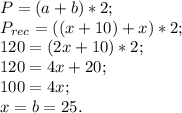
Мы нашли длину стороны b. Отсюда находим сторону a:
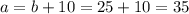
Площадь прямоугольника Srec является произведением длин его сторон:
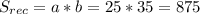
ответ 875 кв. см
Задача 3Купил тетрадей на сумму 8 (шт) * 25 (тг) = 200 (тг),купил ручек на сумму 3 (шт) * 120 (тг) = 360 (тг).ответ: всего потратил 200 + 360 = 560 тг.
Задача 4Дано
Прямоугольник j,его сторона a = 7,его периметр P = 40Найти сторону b
По формуле периметра прямоугольника получаем формулу для нахождения стороны b:
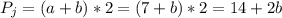
Периметр известен, подставляем его значение в формулу и находим b:
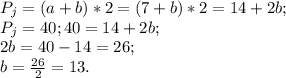
ответ 13
Задача 5Дано
Квадрат с периметром 36 см
Найти его площадь
Решение
Площадь квадрата – это, как бы неловко ни звучало, квадрат его одной стороны.
Введём переменную для стороны квадрата – a. Зная, что стороны квадрата равны, а их 4, работаем с первой известной нам из "Дано" переменной – с периметром. По формуле нахождения периметра квадрата получаем, что сторона a = 9:
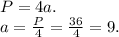
Второй и последний шаг – площадь квадрата. Значения всех необходимых переменных нам теперь известны (сторона):
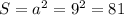
ответ 81 кв. см