

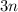 - где n число. Подставим к примеру три натуральных числа вместо n. И получим нужные нам числа:
- где n число. Подставим к примеру три натуральных числа вместо n. И получим нужные нам числа:
 - где m число. Подставим к примеру три натуральных числа вместо m. И получим нужные нам числа:
- где m число. Подставим к примеру три натуральных числа вместо m. И получим нужные нам числа: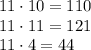
Тогда угол BOC - 4х
Сумма этих углов = 90, т.к. угол АОВ - прямой
х+4х=90
5х=90
х=18 значит, угол АОС - 18 градусов, тогда угол ВОС = 4*18 = 72 градуса
ответ: АОС = 18 градусов, ВОС = 72 градуса