1.
Уравнение плоскости, проходящей через некоторую точку с координатами (x₀,y₀,z₀), в общем виде записывается так:
A(x-x₀) + B(y-y₀) + C(z-z₀)= 0, где коэффициенты A,B,C - координаты вектора нормали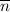 
Найдём вектор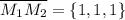 
Вектор нормали 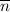найдём из векторного произведения векторов a и M₁M₂
![\overline{n} =[\overline{a}~\times~\overline{M_1M_2}] = \begin{vmatrix} \overline i & \overline j & \overline k \\ 1 & 2 & 1 \\ 1 & 1 & 1 \end{vmatrix} = \overline i - \overline k = \{1, 0, -1\}](/tpl/images/0215/8850/4d6c7.png)
Плоскость задаётся уравнением:
(x - 2) + 0(y - 2) - (z - 1) = 0
ответ: x - z - 1 = 0
2.
Чтобы записать уравнение прямой в каноническом и параметрическом виде необходимо найти направляющий вектор этой прямой и точку, через которую эта прямая проходит
Найдём координаты точки A, которая принадлежит прямой
Пусть z = 0
Решим систему: 
Координаты точки A(-1, 1, 0)
Найдём координаты точки B, которая принадлежит прямой
Пусть z = -4
Снова решим систему: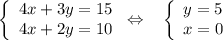 
Координаты точки B(0, 5, -4)
Найдём направляющий вектор прямой
Запишем уравнение прямой в каноническом виде: 
И в параметрическом виде: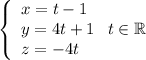 
Размер Масса варенья Количество Всего
банки в одной банке банок варенья
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Большая 500 г 6 шт ?
Маленькая 250 г ? ?
Итого - - 6000 г
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
1) 500 · 6 = 3000 г - в шести больших банках;
2) 6000 - 3000 = 3000 г - оставшееся варенье;
3) 3000 : 250 = 12 шт. - столько маленьких банок понадобится.
ответ: 12 маленьких банок.
2 км =2000 метров
2000 метров-1700 метров=300 метров осталось пробежать
ответ: 300 метров осталось пробежать