1) а = 2 * 2 * 3 * 7 b = 2 * 2 * 3 * 7 a = b
НОК (а; b) = 2 * 2 * 3 * 7 = 84 - наименьшее общее кратное
2) с = 2 * 3 * 3 * 5 d = 2 * 2 * 5
НОК (с; d) = 2 * 2 * 3 * 3 * 5 = 180 - наименьшее общее кратное
3) е = 2 * 3 * 11 f = 2 * 2 * 2 * 3 * 11
НОК (e; f) = 2 * 2 * 2 * 3 * 11 = 264 - наименьшее общее кратное
4) m=2 * 2 * 3 n=2 * 3 * 5
НОК (m; n) = 2 * 3 * 5 * 2 = 60 - наименьшее общее кратное
5) m = 2 * 3 * 5 * 5 n = 2 * 2 * 2 * 2 * 3
НОК (m; n) = 2 * 2 * 2 * 2 * 3 * 5 * 5 = 1200 - наименьшее общее кратное
6) х = 2 * 5 * 11 у = 5 * 5 * 11
НОК (х; у) = 2 * 5 * 5 * 11 = 550 - наименьшее общее кратное
Чтобы найти НОК (а; b), нужно разложить данные числа на простые множители и найти произведение всех простых множителей, взятых с наибольшим показателем степени.
ответ: 20
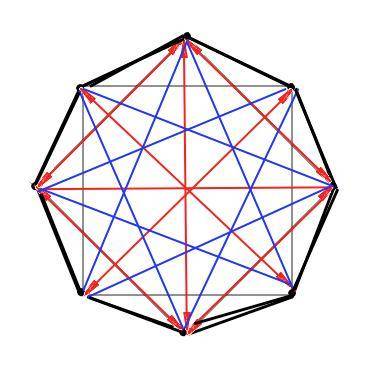
Определение: Диагональ – это отрезок, соединяющий любые две несмежные вершины многоугольника
Объяснение:
Рассмотрим рисунок выпуклого восьмиугольника, данный в приложении. Каждая вершина соединяется отрезками с 7 другими. Но два из этих отрезков не являются диагоналями. Получается, что из каждой вершины выходит диагоналей на 3 меньше, чем количество всех вершин. Для пятиугольника - из каждой вершины выходят 5-3 =2 диагонали. для квадрата из каждой вершины 4-3=1 диагональ. У треугольника диагоналей вовсе нет. Но! Каждая диагональ посчитана дважды ( отмечено на красных диагоналях рисунка). Следовательно, это количество нужно разделить на 2.
Таким образом: формула лля нахождения числа диагоналей многоугольника d =n(n-3)/2, где d – число диагоналей, n – число сторон (вершин) многоугольника.
Число диагоналей восьмиугольника d=8•(8-3)/2=20 ( диагоналей(
составляем уравнение:
х+3х=56
4х=56
х=56:4
х=14 (уч) - мальчиков
14*3=42(уч) - девочки
мальчиков 1 часть, девочек 3 части
1+3=4 части
56:4=14 мальчиков
14*3=42 девочки