Пошаговое объяснение:
1. Апофема - это высота боковой грани, в правильной пирамиде является также её медианой. Также по определению, основанием правильной пирамиды является правильный многоугольник (в данном случае треугольник), и у него равны все стороны.
2. Найти угол наклона апофемы мы можем через прямоугольный треугольник, в котором апофема - это гипотенуза, высота пирамиды - противолежащий катет (1), радиус вписанной в треугольник основания пирамиды окружности - прилежащий катет (2).
Радиус вписанной в правильный треугольник окружности (второй катет) равен 1/3 высоты или (сторона *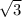 
)/6 (тоже свойство правильного треугольника). То есть (A* 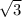)/6
Найдем, первый катет.
3. Первый катет равен по теореме Пифагора корню из разности квадратов бокового ребра пирамиды (то есть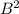 
) и радиуса описанной вокруг основания пирамиды окружности (по свойству правильного треугольника равного (сторона * * 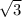)/3 или (A* 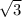)/3).
Первый катет =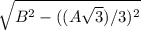 
= 
4. Искомый угол выражается через тангенс, то есть отношение противолежащего (первого) катета к прилежащему (второму) катету:
/ 
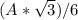
Упрощаем и получаем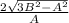 
= tg искомого угла.
ответ: 26; 15; 64;250;24
Пошаговое объяснение:
Делаем задания через определенные интегралы и первообразные:
1.
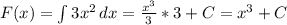
Подставляем в первообразную границы интегрирования:
2.
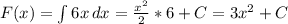
Подставляем в первообразную границы интегрирования:
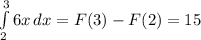
3.
Подставляем в первообразную границы интегрирования:
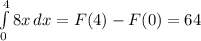
4.
Производим ровно те же операции, что и до этого, так как требуется найти путь у параболы ветвями вверх => интеграл не будет отрицательным.
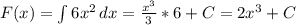
Подставляем в первообразную границы интегрирования:
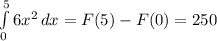
5.
Находим первообразную заданной функции:
Ограничивающие прямые - те же границы интегрирования:
72-17=55( ) вычитаемое!