а)13(x-13)+14(14x-2)=11(3x-11)+28+(10x-21)
13x-169+196x-28=33x-121+28+10x-21
209x-197=43x-114
209x-43x=-114+197
166x=83
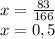
б)-15(15+y)-12(12y+1)+10=16(3y-16)-17(y+17)
-225-15y-144y-12+10=48y-256-17y-289
-227-159y=31y-545
-159y-31y=-545+227
-190y=-318
190y=318

в)18(18-x)-20(2x+20)-8=19(19-3x)-25(x+25)
324-18x-40x-400-8=361-57x-25x-625
-58x-84=-82x-264
-58x+82x=-264+84
24x=-180

г)-21(2x-21)+24(24-3x)-29=30(x+30)-22(-3x-22)
-42x+441+576-72x-29=30x+900+66x+484
-114x+988=96x+1384
-114x-96x=1384-988
-210x=396

Пошаговое объяснение:
1 задача
РЕШЕНИЕ. 1 задача
Введем дискретную случайную величину X = (Число промахов). X может принимать
значения 0, 1, 2, 3, 4
Найдем соответствующие вероятности.
X = 0 , если охотник попал в дичь при первом выстреле, поэтому P(X = 0) = 0,7 .
X =1 , если охотник не попал в дичь при первом выстреле и попал в дичь при втором
выстреле, поэтому P(X =1) = 0,3 ⋅0,7 = 0,21.
X = 2 , если охотник не попал в дичь при первом выстреле и втором выстреле, и попал в
дичь при третьем выстреле, поэтому P(X = 2) = 0,3 ⋅0,3 ⋅0,7 = 0,063 .
X = 3, если охотник не попал в дичь при первом, втором и третьем выстреле, и попал в
дичь при четвертом выстреле, поэтому P(X = 3) = 0,3⋅0,3 ⋅0,3 ⋅0,7 = 0,0189 .
X = 4 , если охотник не попал в дичь при первом, втором, третьем и четвертом выстрелах,
поэтому P(X = 4) = 0,3 ⋅0,3 ⋅0,3 ⋅0,3 = 0,0081.
Закон распределения X :
xi
0
1
2
3
4
pi
0,7
0,21
0,063
0,0189
0,0081
Найдем числовые характеристики с.в. X .
Математическое ожидание:
M ( X ) =∑ xi pi = 0 ⋅0,7 +1⋅0,21+ 2 ⋅0,063+ 3⋅0,0189 + 4 ⋅0,0081 = 0,4251.
Дисперсия:
D( X )
x2=∑ i pi −(M ( X ))2 =0⋅0,7+1⋅0,21+4⋅0,063+9⋅0,0189+16 ⋅0,0081−0,4251 ≈0,581.
ответ:≈0,581.
S квадрата = 9×9=81 дм в квадрате