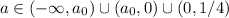, где 
Пошаговое объяснение:
В числителе стоит квадратный трёхчлен, у него может быть не более 2 корней. Значит, чтобы у уравнения было ровно 2 различных корня, числитель должен иметь 2 корня, и ни один из корней числителя не должен быть корнем знаменателя.
У числителя два неравных корня, если дискриминант больше нуля:
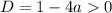
Найдём, при каких a хотя бы какой-то корень числителя является корнем знаменателя:
Подставляем найденный x в уравнение:
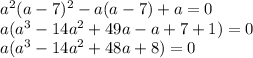
Один корень (a = 0) находится легко, еще один корень можно выписать по формулам для кубических уравнений или найти графически. Можно показать, что что этот корень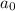 
единственный и удовлетворяет неравенству 1 - 4a > 0: производная функции 
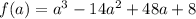равна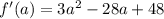 
. При a < 1/4 производная положительна, кроме того, 
, 
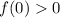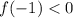, поэтому f(a) имеет корень на отрезке [-1, 0]. Выражение для 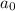довольно-таки громоздкое, по графику
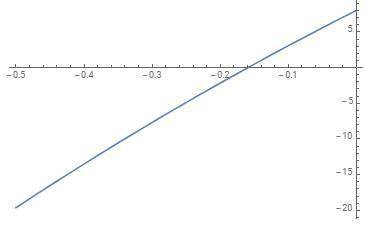
P=640cм=64дм
найдем ширину первого прямоуголника
р=2(a+b)
p=2a+2b
b=(p-2a)/2=(64-2*12)/2=20дм
найдем ширину второго прям.-ка по той же формуле
b=(64-2*10)/2=22дм
найдем площади
а)первого прям-ка
s1=a*b=12*20=240дм в квадрате
б)второго прям-ка
s2=22*10=220дм в квадрате
s1>s2
ответ:у первого прямоугольника площадь больше
2)найдем сторону квадрата из формулы площади квадрата
S=a^2
a=корень из S
a=корень из 3600=60см
найдем ширину прямоугольника из формулы площади прям-ка
s=a*b
b=s/a=3600/90=40cм
найдем периметр этих фигур
квадрата: P1=4*60=240
прям-ка: P2=(40+90)*2=260
У прям-ка больше периметр
