1. Начертите отрезок, равный стороне. Левый конец отрезка обозначьте буквой А, а правый конец отрезка - буквой С.
2. Возьмите транспортир установите его диаметром на отрезок АС так, центр окружности транспортира совпадал с точкой А, поставьте на бумаге точку, соответсвующие первому углу на транспортире.
3. Проведите линию через точку А и точку, соответсвующие отмеренному первому углу. Не скупитесь, пусть эта линия будет продолжена далеко за точку угла.
4. Возьмите транспортир установите его диаметром на отрезок АС так, центр окружности транспортира совпадал с точкой С, поставьте на бумаге точку, соответсвующие второму углу на транспортире.
5. Проведите линию через точку С и точку, соответсвующие второму отмеренному углу. Не скупитесь, пусть эта линия будет продолжена далеко за точку угла.
6. Отметьте точку пересечений линий, построенных при транспортира. Обозначьте эту точку буквой В.
Треугольник АВС по стороне и двум углам построен.
1) Функция определена повсюду кроме точки, в которой знаменатель превращается в ноль, x = 0.
Область определения состоит из двух интервалов D(y):(-∞;0) U (0; +∞).
2) Так как функция не имеет значения при х = 0, то график функции не пересекает ось Оу.
Приравняем функцию к нулю:
1/3x=0.
Так как эта функция не может быть равна 0, то график функции не пересекает ось Ох:
3) Проверяем функцию на четность.
Проверим функцию - четна или нечетна с соотношений f(x)=f(-x) и f(x)=-f(x). Итак, проверяем:
f(-x)=1/(3*(-x))=-1/3x≠f(x)=-f(x).
Итак, функция нечетная, непериодическая.
4) В данном случае имеем одну точку разрыва x=0.
Вычислим границы слева и справа от этой точки
lim┬(x→-0)〖 1/3x=-∞.〗
lim┬(x→+0)〖 1/3x=+∞.〗
Итак, x=0 – точка разрыва второго рода.
5) Для отыскания интервалов монотонности вычисляем первую производную функции
〖y^'=〗〖1/3* -1/x^2 =-1/〖3x〗^2 =0.〗
Решаем это уравнение и его корни будут экстремумами, но так как переменная только в знаменателе, то производная не может быть равна нулю.
Поэтому функция не имеет экстремумов.
Поскольку при любых значениях аргумента производная отрицательна, то функция на всей области убывающая.
6. Точки перегибов графика функции:
Найдем точки перегибов для функции, для этого надо решить уравнение y''=0 - вторая производная равняется нулю, корни полученного уравнения будут точками перегибов указанного графика функции, + нужно подсчитать пределы y'' при аргументе, стремящемся к точкам неопределенности функции:
y''((1/(3x)) = 2/(3x³) = 0
Данная функция не может быть равна нулю, поэтому перегибов у функции нет.
7) Интервалы выпуклости и вогнутости.
Интервалы, где функция выпуклая или вогнутая, находим по знаку второй производной : где вторая производная меньше нуля, там график функции выпуклый, а где больше - вогнутый.
x = -1 0 1
y'' = -2/3 - 2/3.
Вогнутая на промежутках: (0; ∞)
Выпуклая на промежутках: (-∞;0)
8) Асимптоты.
Вертикальной асимптотой является ось Оу, определённая в пункте 4.
Горизонтальные асимптоты графика функции:
Горизонтальную асимптоту найдем с предела данной функции при x->+∞ и x->-∞. Соотвествующие пределы находим:
lim┬(x→∞)〖 1/3x=∞〗, значит, горизонтальной асимптоты справа не существует.
Аналогично, при x->-∞ f(x) = -∞, значит, горизонтальной асимптоты слева не существует
Наклонные асимптоты графика функции.
Уравнение наклонной асимптоты имеет вид y=kx+b. Наклонную асимптоту можно найти, подсчитав предел данной функции, деленной на x при lim┬( x→±∞)〖(kx+b-f(x)).〗
Находим коэффициент k: k=lim┬(x→±∞)〖(f(x))/x.〗
k=lim┬( x→±∞)〖 1/(3x*x)=1/〖3x〗^2 =0.〗
Коэффициент b: b=〖lim┬(x→±∞) (〗〖f(x)-kx).〗
Для данной функции первый из этих пределов равен нулю, поэтому наклонная линия не определяется (она совпадает с горизонтальной асимптотой).
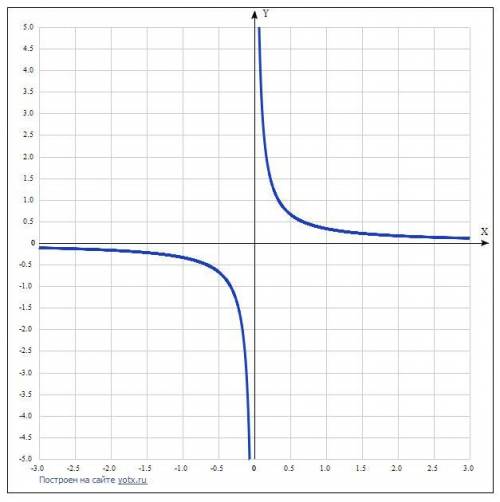
8) На основе проведенного анализа выполняем построение графика функции. Для этого сначала строим вертикальные и наклонные асимптоты, затем находим значение функции в нескольких точках и по них проводим построение.
Таблица точек
x y
-3.0 -0.11
-2.5 -0.13
-2.0 -0.17
-1.5 -0.22
-1.0 -0.33
-0.5 -0.67
0 -
0.5 0.67
1.0 0.33
1.5 0.22
2.0 0.17
2.5 0.13
3.0 0.11.
100-36=64
ответ: в конструкторе на 64 больше брусков, чем других деталей