Найдите значение выражения: (1,3-2 1/4: 0,9)x(-10)-13 по действиям надо

👇

Увидеть ответ

Ответ:

flag4

24.04.2023

1) 2 1/4:0,9=2,5
2)1,3-2,5=-1,2
3)-1,2•(-10)=12
4)12-13=-1
ответ: -1.

4,4(38 оценок)

Открыть все ответы

Ответ:

yusulimanov00

24.04.2023

Пусть расстояние от Васильково до Ромашково равно s км.

Обозначим скорости автомобилей А, В и С - x, y и z соответственно.

По условию, автомобиль В, доехав до Ромашково, сразу повернул назад и встретил автомобиль Б в 18 км от Ромашково. Значит, автомобиль В проехал к тому моменту (s+18) км, а автомобиль Б - (s-18) км. Но на это они затратили одинаковое время, значит:

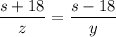
$\dfrac{s+18}{z} =\dfrac{s-18}{y}$

По условию, автомобиль В, доехав до Ромашково, сразу повернул назад и встретил автомобиль А в 25 км от Ромашково. Значит, автомобиль В проехал к тому моменту (s+25) км, а автомобиль A - (s-25) км. Но на это они затратили одинаковое время, значит:

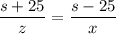
$\dfrac{s+25}{z} =\dfrac{s-25}{x}$

Наконец, по условию, автомобиль Б, доехав до Ромашково, сразу повернул назад и встретил автомобиль А в 8 км от Ромашково. Значит, автомобиль Б проехал к тому моменту (s+8) км, а автомобиль A - (s-8) км. Но на это они затратили одинаковое время, значит:

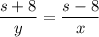
$\dfrac{s+8}{y} =\dfrac{s-8}{x}$

Получаем следующую систему:

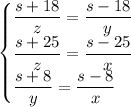
$\begin{cases} \dfrac{s+18}{z} =\dfrac{s-18}{y} \\ \dfrac{s+25}{z} =\dfrac{s-25}{x} \\ \dfrac{s+8}{y} =\dfrac{s-8}{x}\end{cases}$

Из второго уравнения выразим z:

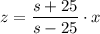
$z=\dfrac{s+25}{s-25}\cdot x$

Из третьего уравнения выразим y:

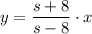
$y= \dfrac{s+8}{s-8} \cdot x$

Подставим полученные соотношения в первое уравнение:

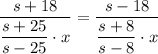
$\dfrac{s+18}{\dfrac{s+25}{s-25}\cdot x} =\dfrac{s-18}{ \dfrac{s+8}{s-8} \cdot x}$

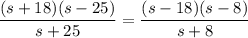
$\dfrac{(s+18)(s-25)}{s+25} =\dfrac{(s-18)(s-8)}{s+8}$

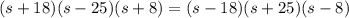
(s+18)(s-25)(s+8)=(s-18)(s+25)(s-8)

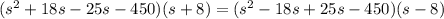
(s^2+18s-25s-450)(s+8)=(s^2-18s+25s-450)(s-8)

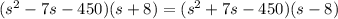
(s^2-7s-450)(s+8)=(s^2+7s-450)(s-8)

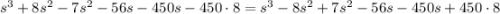
$s^3+8s^2-7s^2-56s-450s-450\cdot8=s^3-8s^2+7s^2-56s-450s+450\cdot8$

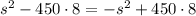
$s^2-450\cdot8=-s^2+450\cdot8$

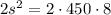
$2s^2=2\cdot450\cdot8$

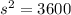
s^2=3600

s=60 (отрицательный корень не удовлетворяет смыслу задачи)

ответ: 60 км

4,6(30 оценок)

Ответ:

taklecovatana

24.04.2023

√3

Пошаговое объяснение:

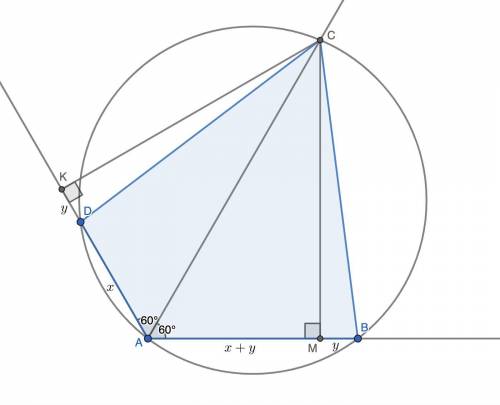
Не теряя общности, положим AD ≤ AB. Опустим перпендикуляры CK и CM на стороны угла. Обозначим AD = x, DK = y.

Так как AC — биссектриса, точка C равноудалена от сторон угла, то есть CK = CM. Прямоугольные треугольники AKC и AMC равны по катету (CK = CM) и гипотенузе (AC — общая) ⇒ AK = AM = x + y.

Так как ∠DAC = ∠BAC, DC = BC как хорды, на которые опираются равные углы. Прямоугольные треугольники DKC и BMC равны по катету (CK = CM) и гипотенузе (DC = BC) ⇒ DK = BM = y.

По условию AB + AD = (x + y + y) + x = 2(x + y) = 2 ⇒ x + y = 1. Тогда AM = x + y = 1. В прямоугольном треугольнике AMC ∠ACM = 90° - ∠CAM = 90° - 60° = 30°. По теореме об угле в 30° AC = 2AM = 2.

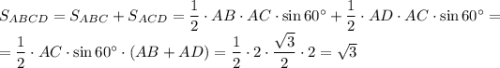
$S_{ABCD}=S_{ABC}+S_{ACD}=\dfrac{1}{2}\cdot AB\cdot AC\cdot\sin{60^{\circ}}+\dfrac{1}{2}\cdot AD\cdot AC\cdot\sin{60^{\circ}}=\\=\dfrac{1}{2}\cdot AC\cdot\sin{60^{\circ}}\cdot (AB+AD)=\dfrac{1}{2}\cdot 2\cdot\dfrac{\sqrt{3}}{2}\cdot 2=\sqrt{3}$