Question

Центром квадрата является точка (2; -1) , а две смежные стороны расположены на прямых y= x - 1 и y= -x - 1 . начерти этот квадрат и найди, какими линейными функциями заданы две другие стороны квадрата.

Answer 1

Точка пересечения прямых y= x - 1 и y= -x - 1 даёт одну вершину квадрата.
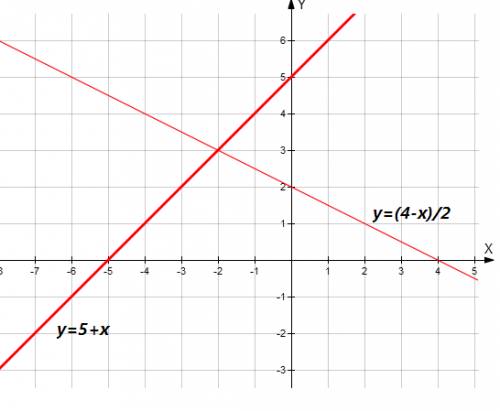
 x - 1 = -x - 1 
2х = 0
х = 0     у = 0 - 1 = -1.
Пусть это будет точка А(0; -1)
Так как точка А и центр квадрата (точка О) имеют одинаковое значение по оси ординат, то диагональ квадрата параллельна оси Х.
Точка С симметрична точке А:
Хс = 2Хо - Ха = 2*2 - 0 = 4.
Точка С(4; -1).
Вторая диагональ будет параллельна оси У. Так как половина диагонали равна 4/2 = 2 единицы, то координаты точек В и Д по оси Х равны точке О, а по оси У -+-2 единицы:
В(2; -1+2 = 1) = (2; 1).
Д(2; -1-2 = -3) = (2; -3).

Прямая ВС параллельна АД, поэтому имеет коэффициент а =-1. Её уравнение у = -х + в.
Подставив координаты точки В в это уравнение , находим значение в:
1 = -2 + в    в = 1 + 2 = 3.
Уравнение ВС: у = -х + 3.

Аналогично определяем уравнение СД:
у = х + в
Подставив координаты точки Д в это уравнение , находим значение в:
-3 = 2 + в    в = -3 - 2 = -5.
Уравнение СД: у = х - 5.

Квадрат строится по полученным координатам точек А, В, С и Д.