В первой стопке 40 журналов, а во второй — 30.
Пошаговое объяснение:
Если бы в первой стопке было бы столько же журналов сколько и во второй, то сумма журналов была бы:
70 - 10 = 60 — общее количество журналов в двух одинаковых стопках.
Таким образом мы уравняли количество журналов в обеих стопках. Теперь, разделив 60 на количество стопок, можно узнать сколько журналов во второй стопке:
60 : 2 = 30 журналов.
Чтобы узнать, сколько журналов в первой стопке, надо вернуть обратно 10 журналов в первую стопку:
30 + 10 = 40 журналов.
Решение задачи по действиям можно записать так:
1) 70 - 10 = 60 — общее количество журналов в двух одинаковых стопках.
2) 60 : 2 = 30 — количество журналов во второй стопке.
3) 30 + 10 = 40 — количество журналов в первой стопке.
Можно выполнить проверку и убедиться, что задача решена правильно:
40 + 30 = 70 — общее количество журналов,
40 - 30 = 10 — разница в количестве журналов между стопками.
№1.
30 - 17 = 13 девочек в классе
13/30 части класса - составляют девочки
13 - числитель; 30 - знаменатель.
№2.
а) 1 кг = 1 000 г
1 000 * 1/2 = 1000 : 2 = 500 г
1 000 * 3/5 = 1 000 : 5 * 3 = 600 г
б) 1 м = 100 см
100 * 1/4 = 100 : 4 = 25 см
100 * 7/10 = 100 : 10 * 7 = 70 см
в) 1 мин. = 60 сек.
60 * 1/6 = 60 : 6 = 10 сек.
60 * 2/3 = 60 : 3 * 2 = 40 сек.
№3.
2/3 к знаменателю 12:
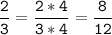
2/3 к знаменателю 15:

2/3 к знаменателю 36:
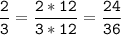
К наименьшему общему знаменателю:
3/5 и 2/3:
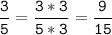

ответ: 9/15 и 10/15
3/4 и 5/16:
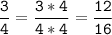
ответ: 12/16 и 5/16
1/4 и 1/6:


ответ: 3/12 и 2/12.
№4.
41/100 нельзя сократить, т.к. 41 является простым числом, т.е. делится только на 1 и само себя.
Еще примеры несократимых дробей:
3/5; 13/20; 17/100; 23/50; 47/50; 107/200.
Сократим дроби:
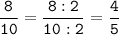


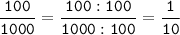
№5.
Чтобы сравнить дроби, нужно привести их к общему знаменателю:
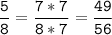

5/8 > 4/7 , т.к. 49/56 > 32/56
Правильная дробь всегда меньше неправильной:
7/10 < 10/7.
№6.
3 : 5 = 3/5
20 : 25 = 20/25 = 4/5
m : n = m/n
2)0,6*14= 8,4(км) проехал второй велосипедист
3) 6,6+8,4=15(км)расстояние между поселками
ответ: 15 км