Пошаговое объяснение:
Пусть X и Y - какие-то множества. Имеет место функция, определённая на множестве X со значениями на множестве Y, если в силу некоторого закона f каждому элементу x∈X ставится в соответствие один и только один элемент y∈Y.
Это записывается в виде
y = f(x).
Другими словами, с функции y = f(x) множество X отображается в множество Y. Поэтому функцию называют также отображением.
Например, авиапассажиры сидят в креслах салона пассажирского самолёта. Пусть X - множество пассажиров, а Y - множество кресел салона. Тогда возникает соответствие f : каждому пассажиру x∈X сопоставляется то кресло y = f(x), в котором он сидит.
Наблюдается, таким образом, простой пример функции, областью определения которой является множество X пассажиров, а областью значений - множество f(X) занимаемых ими кресел. Если заполнены не все кресла Y, то множество значений функции будет подмножеством Y, не совпадающим со всем множеством Y.
Если в кресле находятся два пассажира и (например, мать и ребёнок), то это никак не противоречит определению функции f, которая и , и однозначно ставит в соответствие кресло . При этом такая функция принимает одно и то же значение при разных значениях и аргумента, подобно тому как числовая функция y = f(x) = x² принимает одно и то же значение 9 при x = - 3 и при x = 3.
Если, однако, какому-то пассажиру удастся сесть сразу в два кресла и , то нарушится принцип однозначной определённости значений функции, поэтому такая ситуация не является функциональной в смысле данного выше определения функций, поскольку требуется, чтобы каждому значению x аргумента соответствовало бы одно определённое значение y = f(x) функции.
В математическом анализе часто X обозначают как D (область определения функции), а Y как E (область значений функции) и при этом D и E называют подмножествами R (множества действительных чисел). На сайте есть урок Как найти область определения функции.
Как нетрудно догадаться по названию нашего сайта, он назван так в честь функции от икса или f(x). И это неслучайно. Функции составляют бОльшую часть предметов рассмотрения не только математического анализа, но и дискретной математики, а также широко используются в программировании, где от профессионалов требуется выделять однотипные вычисления в функции.
Пример 1. Даны множества A = {a, b, c, d, e} и L = {l, m, n}. Можно ли между элементами этих множеств установить такое соответствие, чтобы оно было функцией? Если да, то записать это соответствие, указав стрелками, какой элемент какому соответствует.
Решение. Итак, множество A содержит 5 элементов, а множество L - 3 элемента. Если мы поставим стрелки, ведущие от каждого элемента множества L к элементам множества A, то некоторым элементам L будут соответствовать более одного элемента A. Такое соответствие не является функцией по определению. Но если мы проведём стрелки от элементов A к элементам L, то некоторым элементам A будут соответствовать одни и те же элементы L, но при этом каждому элементу A будет соответствовать не более одного элемента L. Такое соответствие не противоречит определение функции, следовательно, ответ на вопрос задания - положительный.
Можно задать, например, такое соответствите между элементами данных множеств, которое будет функцией:
Пошаговое объяснение:
ДАНО: Y = x³/(x-1)
Исследование
1. Область определения: D(х)= R\{1} = (-∞;1)∪(1;+∞).
Не допускаем деления на 0 в знаменателе.
2.Поведение в точке разрыва. LimY(1-)= -∞, LimY(1+)= +∞. Вертикальная асимптота - х = 1. Неустранимый разрыв II-го рода.
3. Поведение на бесконечности - наклонная асимптота.
k = lim(+∞)Y(х)/x = х³/(x²+ x) = ∞ - коэффициент наклона.
Наклонной асимптоты нет.
4. Нули функции, пересечение с осью ОХ. Y(x) = 0.
5. Пересечение с осью ОУ. Y(0) = 0
6. Интервалы знакопостоянства.
Отрицательна: Y(x)<0 - X∈(0;1).
Положительна: Y>0 - X∈(-∞;0)∪(1;+∞)
7. Проверка на чётность.
Функция со сдвигом от осей симметрии - функция общего вида.
Ни нечётная: Y(-x) ≠ -Y(x) ни чётная: Y(-x) ≠ Y(x)
8. Поиск экстремумов по первой производной.
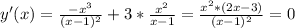
Корни квадратного уравнения. х1 = 0 и х2= 3/2 = 1,5.
9. Локальные экстремумы.
Минимум: Y(1,5) = 6.75 , Максимум: Y(0) = 0
10. Интервалы монотонности.
Возрастает: X∈(1.5;+∞)
Убывает: Х∈(-∞;1)∪(1;1.5)
11. Поиск перегибов по второй производной.
y''(x) = 2*x*(x²-3*x+3)/(x-1)² = 0
x = 0 и точка разрыва при Х = 1.
12. Выпуклая - 'горка' - X∈(0;1).
Вогнутая - 'ложка'- X∈(-∞;0)∪(1;+∞;).
13. Область значений. E(y) - y∈(-∞;+∞).
Рисунок с графиком функции в приложении.

Вероятность ПЕРВОГО брака = 5/30 = 1/6
и УМНОЖАЕМ на вероятность ВТОРОГО брака = 4/29
и получаем
Р2 = 1/6*4/29 = 2/87 ~ 0.023 ~ 2.3% - ОТВЕТ
Задача 3.
0,6 и 0,7 - работают и 0,4 и 0,3 - отказ
а) сработают ОБА - событие "И" - произведение вероятностей.
Ра = 0,4*0,3 = 0,12 = 12%
б) событие "ИЛИ" первый или второй
Рб = p1*q2 + q1*p2 = 0,6*0,3 + 0,4*0,7 = 0,18 + 0,28 = 0,46 = 46% - ОТВЕТ
Задача 4
Одно из двух - событие "ИЛИ" суммируем
Р4 = 0,8*0,2 + 0,2*0,8 = 2*0,16 = 0,32 =32% - ОТВЕТ
Задача 6
События "И" три раза
Р6 = 20/25 * 19/24 * 18/23 = 57/115 ~ 0.4956 ~ 49.6% - ОТВЕТ