Question

Найти сумму действительных корней уравнения:

Answer 1

Используем метод неопределённых коэффициентов.Предположим, что левая часть уравнения разлагается на множители второй степени с целыми коэффициентами. Обозначим один из них через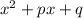 $x^2+px+q$, другой - через $x^2+rx+s$.

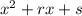Задача сводится к нахождению p, q, r, s. Тогда

$x^4-2x^2-12x-8=(x^2+px+q)(x^2+rx+s)=0$

$\begin{cases} p+r=0\\q+s+pr=-2\\ps+qr=-12\\qs=-8 \end{cases}$

Можно попробовать взять q=4, s=-2, тогда p=2, r=-2, а уравнение может быть представлено в виде: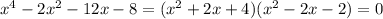 $x^4-2x^2-12x-8=(x^2+2x+4)(x^2-2x-2)=0$

$x^2+2x+4=0$ не имеет действительных корней, так как дискриминант меньше 0 (2^2-4*4=-12).

$x^2-2x-2=0$

$x_1=(2+\sqrt{12})/2=1+\sqrt{3}$

$x_2=(2-\sqrt{12})/2=1-\sqrt{3}$

Сумма корней: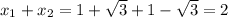 $x_1+x_2=1+\sqrt{3}+1-\sqrt{3}=2$

если взять q=-4, s=2, тогда p=-2, r=2, а уравнение может быть представлено в виде: $x^4-2x^2-12x-8=(x^2-2x-4)(x^2+2x+2)=0$

$x^2-2x-4=0$

$x_1=(2+\sqrt{20})/2=1+\sqrt{5}$

$x_2=(2-\sqrt{20})/2=1-\sqrt{5}$

$x^2+2x+2=0$ не имеет действительных корней, так как дискриминант меньше 0 (2^2-4*2=-4).

Сумма корней: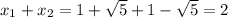 $x_1+x_2=1+\sqrt{5}+1-\sqrt{5}=2$

ответ: 2.