Математика: Сколько всего времени(секунд) в трех днях?

Сколько всего времени(секунд) в трех днях?

👇

Увидеть ответ

Ответ:

turansalehova

27.02.2022

60х60=3600( в одном часе)
3600х24=86400(в одном дне)
86400х3=259200(3 дня)

4,4(90 оценок)

Ответ:

Машина0

27.02.2022

1 день=24 ч.
24 ч.=1440 мин =86 400 секунд
3 дня= 3*86 400=259 200 секунд

4,7(98 оценок)

Открыть все ответы

Ответ:

kantuz

27.02.2022

Начнем строить цепочку.

Удобно начать с числа 16, так как это наибольшее число. Даже если рядом с ним поставить число 15, то их сумма даст 31, а значит все потенциальные квадраты должны быть не больше 31.

Итак, от 16 до 31 есть только один квадрат: 25. Значит, дополняем число 16 до 25 числом 9:

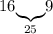
$16 \underset{25}{\underbrace{}} 9$

Число 9 до 25 мы только что дополняли, значит остается только дополнить его до 16 - числом 7:

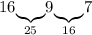
$16 \underset{25}{\underbrace{}} 9\underset{16}{\underbrace{}}7$

Число 7 до 25 дополнить не можем (числа 18 среди карточек нет), значит остается дополнить его до 9 - числом 2:

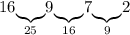
$16 \underset{25}{\underbrace{}} 9\underset{16}{\underbrace{}}7\underset{9}{\underbrace{}}2$

Число 2: до 4 дополнить не можем, так как нужное в этом случае число 2 занято, до 9 дополняли только что, остается дополнить его до 16 - числом 14:

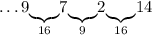
$\ldots9\underset{16}{\underbrace{}}7\underset{9}{\underbrace{}}2\underset{16}{\underbrace{}}14$

Число 14: до 16 дополнить не можем, так как нужное в этом случае число 2 занято, остается дополнить его до 25 - числом 11:

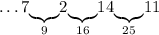
$\ldots7\underset{9}{\underbrace{}}2\underset{16}{\underbrace{}}14\underset{25}{\underbrace{}}11$

Число 11: можем дополнить только до 16 - числом 5:

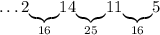
$\ldots2\underset{16}{\underbrace{}}14\underset{25}{\underbrace{}}11\underset{16}{\underbrace{}}5$

Число 5: можем дополнить только до 9 - числом 4:

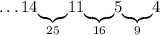
$\ldots14\underset{25}{\underbrace{}}11\underset{16}{\underbrace{}}5\underset{9}{\underbrace{}}4$

Число 4: можем дополнить только до 16 - числом 12:

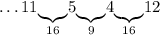
$\ldots11\underset{16}{\underbrace{}}5\underset{9}{\underbrace{}}4\underset{16}{\underbrace{}}12$

Число 12: можем дополнить только до 25 - числом 13:

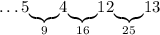
$\ldots5\underset{9}{\underbrace{}}4\underset{16}{\underbrace{}}12\underset{25}{\underbrace{}}13$

Число 13: можем дополнить только до 16 - числом 3:

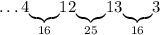
$\ldots4\underset{16}{\underbrace{}}12\underset{25}{\underbrace{}}13\underset{16}{\underbrace{}}3$

Число 3. Только на этом шаге возникает несколько вариантов. Мы можем дополнить его до 4 или до 9. Пробуем дополнить до 4 - числом 1:

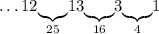
$\ldots12\underset{25}{\underbrace{}}13\underset{16}{\underbrace{}}3\underset{4}{\underbrace{}}1$

Число 1. Опять же, мы можем дополнить его до 9 или до 16. Пробуем дополнить до 9 - числом 8:

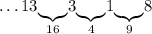
$\ldots13\underset{16}{\underbrace{}}3\underset{4}{\underbrace{}}1\underset{9}{\underbrace{}}8$

Число 8. До 9 его мы дополняли только что, до 16 дополнить его не можем (отсутствует еще одна восьмерка), до 25 также дополнить не можем (карточки 17 у нас нет). Тупик.

Значит, нужно вернуться назад и попробовать дополнить число 1 до 16 - числом 15:

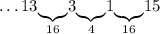
$\ldots13\underset{16}{\underbrace{}}3\underset{4}{\underbrace{}}1\underset{16}{\underbrace{}}15$

Число 15: можем дополнить только до 25 - числом 10:

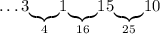
$\ldots3\underset{4}{\underbrace{}}1\underset{16}{\underbrace{}}15\underset{25}{\underbrace{}}10$

Число 10: можем дополнить только до 16 - числом 6:

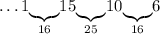
$\ldots1\underset{16}{\underbrace{}}15\underset{25}{\underbrace{}}10\underset{16}{\underbrace{}}6$

Число 6. Для дополнения его до 9 нам нужна карточка 3, а она занята, до 16 мы его дополняли только что. Вновь тупик.

В этом случае, снова возвращаемся назад и дополняем число 13 до 9 - числом 6:

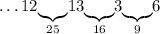
$\ldots12\underset{25}{\underbrace{}}13\underset{16}{\underbrace{}}3\underset{9}{\underbrace{}}6$

Число 6: можем дополнить только до 16 - числом 10:

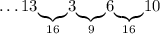
$\ldots13\underset{16}{\underbrace{}}3\underset{9}{\underbrace{}}6\underset{16}{\underbrace{}}10$

Число 10: можем дополнить только до 25 - числом 15:

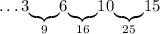
$\ldots3\underset{9}{\underbrace{}}6\underset{16}{\underbrace{}}10\underset{25}{\underbrace{}}15$

Число 15: можем дополнить только до 16 - числом 1:

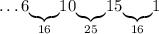
$\ldots6\underset{16}{\underbrace{}}10\underset{25}{\underbrace{}}15\underset{16}{\underbrace{}}1$

Число 1: дополняем единственным оставшимся числом 8 - до 9:

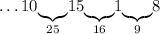
$\ldots10\underset{25}{\underbrace{}}15\underset{16}{\underbrace{}}1\underset{9}{\underbrace{}}8$

Таким образом, ряд чисел составить получилось:

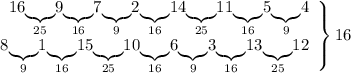
$\left\begin{array}{r}16 \underset{25}{\underbrace{}} 9\underset{16}{\underbrace{}}7\underset{9}{\underbrace{}}2\underset{16}{\underbrace{}}14\underset{25}{\underbrace{}}11\underset{16}{\underbrace{}}5\underset{9}{\underbrace{}}4 \\ 8\underset{9}{\underbrace{}}1\underset{16}{\underbrace{}}15\underset{25}{\underbrace{}}10\underset{16}{\underbrace{}}6\underset{9}{\underbrace{}}3\underset{16}{\underbrace{}}13\underset{25}{\underbrace{}}12\end{array}\right\}16$

Однако, этот ряд не закольцовывается, так как сумма первого и последнего элемента равна 24 и не является квадратом.

Таким образом, выложить в ряд у Васи получится, а выложить по кругу у Пети не получится.

ответ: у Пети - нет, у Васи - да

4,7(73 оценок)

Ответ:

ирина1523

27.02.2022

Два сомножителя должны заканчиваться на 3 и 7, либо оба на 1, либо оба на 9.

Алгоритм построения сомножителей рассмотрим на примере поиска подходящего сомножителя для числа 7, например:

* 7

Далее начинаем заполнять верхний ряд справа налево, неизменно получая в результате очередные 0 или 1.

2) 2 - в уме. значит следующее произведение должно оканчиваться либо на 9, либо на 8. На 8 -произведение любого числа на 7 не заканчивается. Поэтому вариант один:

---73

* 7

3) 5 - в уме. Значит следующее произведение должно заканчиваться либо на 5, либо на 6. Поставим цифру 5.

--573

* 7

011

4) 4 - в уме. Видно что поставив теперь цифру 1, сразу получим 11 - две недостающие единицы.

1573

* 7

11011

По такому алгоритму подбирается состав сомножителей.

Указанное число дают в произведении:

77*143, 121*91, 11*1001, 847*13

Кроме того, несколько очевидных вещей:

Сомножители нечетные, не делятся на 3 и 5, раскладываются на простые множители с нужными окончаниями: 7,11,13...

Может я что-то не понял - окаких закономерностях идет речь???

Я описал алгоритм получения сомножителей. Может об этом и идет речь. Если это неправильно, можешь написать модератору, пусть снимут баллы. Мне истина дороже.

4,5(72 оценок)

Это интересно:

Питомцы-и-животные

10.09.2021

Как разводить лягушек: советы для начинающих...

Стиль-и-уход-за-собой

11.03.2022

5 простых шагов, как сделать маску для лица из алоэ вера...

Компьютеры-и-электроника

02.01.2020

Использование Wi-Fi Direct на Android: инструкция для начинающих...

Семейная-жизнь