ответ: Увеличение на: 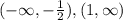
Убывает на: 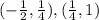 .
.
Пошаговое объяснение: Найдем производную.
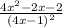
Приравняем производную к 0.
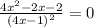
Решим относительно x.
Упростим числитель.
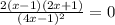
Найдем НОЗ членов уравнения.

Умножим каждый член на  и упростим.
и упростим.
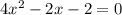
Решим уравнение.
Разлагаем на множители левую часть уравнения.
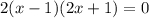
Разделим обе части уравнения на 2. Результат деления 0 на любое ненулевое значение равен 0.
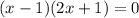
Приравняем x-1 к 0, затем решим относительно x.
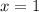
Приравняем 2x+1 к 0, затем решим относительно x.
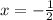
Решение является результатом x-1=0 и 2x+1=0.
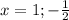
Значения, которые обращают производную в 0 - 1,  .
.
1,  .
.
Выясним, при каких значениях переменной функция 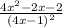 не определена.
не определена.
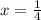
Разобьем 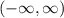 на интервалы вокруг значений x, в которых производная равна 0 или не определена.
на интервалы вокруг значений x, в которых производная равна 0 или не определена.
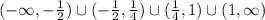
Подставим значение из интервала 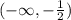 в производную, чтобы определить, возрастает или убывает функция.
в производную, чтобы определить, возрастает или убывает функция.
Увеличение на 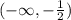 , так как
, так как 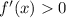 .
.
Подставим значение из интервала 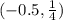 в производную, чтобы определить, возрастает или убывает функция.
в производную, чтобы определить, возрастает или убывает функция.
Убывает на 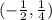 , поскольку
, поскольку 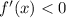
Подставим значение из интервала (0.25, 1) в производную, чтобы определить, возрастает или убывает функция.
Убывает на 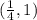 , поскольку
, поскольку 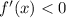
Подставим значения из интервала 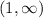 в производную, чтобы определить, возрастает или убывает функция.
в производную, чтобы определить, возрастает или убывает функция.
Увеличение на 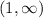 , так как
, так как 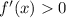 .
.
Перечислим промежутки, на которых функция возрастает и убывает.
Увеличение на: 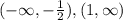
Убывает на: 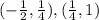
100
Пошаговое объяснение:
Пусть мандарины раздавали детям, которых было х. Тогда, если раздавать их детям по 5 мандаринов каждому, то не хватит 4 мандаринов, а значит было мандаринов 5х - 4. В случае, если раздать по 4 мандарина, то в пакете останется 16 мандаринов: 4х + 16.
В двух случаях количество мандаринов равное:
5х - 4 = 4х + 16.
В правой части собираются слагаемые с неизвестной величиной, а в левой - свободные члены:
5х - 4х = 16 + 4.
х = 20 - детей получали мандарины.
В пакете было 4 * 20 + 16 = 100 мандаринов.
1дм=10 см
1м=100см
100Х10=90