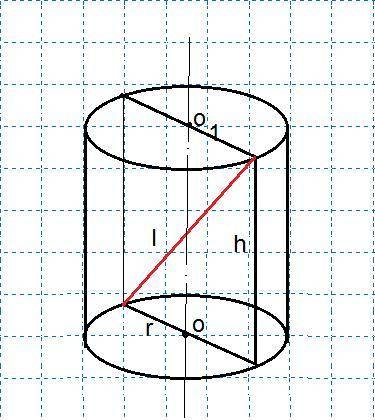
1. Высота цилиндра равна (по теореме Пифагора) h=√(l²-D²), где l - диагональ осевого сечения, а D - диаметр основания цилиндра.
1) 4×2=8 см - диаметр цилиндра
2) √(10²-8²)=√36=6 см - высота цилиндра
Площадь осевого сечения (прямоуг.) находим по формуле S=Dh.
3) 6×8=48 см² - площадь осевого сечения (см. рис в приложении)
2. Площадь боковой поверхности конуса находится по формуле S(b) = πRL, где R - радиус основания, а L - образующая.
1) 3,14×4×20=251,2 см² - площадь боковой поверхн. цилиндра
Полная площадь цилиндра находится по формуле S(p) = πRL + πR², где πR² - площадь основания (круга).
2) 3,14×4²=50, 24 см² - площадь основания
3) 251,2+50,24=301,44 см² - полная площадь цилиндра
36
Пошаговое объяснение:
Мы знаем, что площадь боковой поверхности треугольной пирамиды состоит из трёх треугольников. Следовательно, нам можно найти площадь одного из таких треугольников и умножить его на 3, т.к. наша пирамида правильная. А площадь треугольника находится по формуле (h*AB)/2, где h - высота треугольника, а AB - основание.
Исходя из условия, мы получаем, что все боковые рёбра равны 4 (BS = 4), потому что пирамида правильная. Берём одну грань пирамиды ( треугольник с основанием AB). Т. к. всё боковые рёбра нашей пирамиды равны, то треугольник получается равнобедренным, а SR является и медианой, и биссектрисой, и высотой. Итак, все измерения мы нашли, поэтому смело можем находить площадь этой грани. (SR*AB)/2= (6*4)/2 = 12. А чтобы найти площадь всей боковой поверхности, мы умножаем 12 на 3 (три грани у нас). ответ: 36
S = 1/2 * (2*-6 - 7*-5)
S = 1/2 * (-12+35)
S = 1/2 * 23
S = 11,5
ответ: 11,5