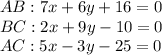
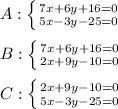
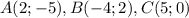
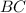 как уравнение с угловым коэффициентом:
как уравнение с угловым коэффициентом: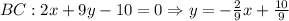
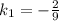
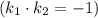 найдем
найдем 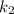 – угловой коэффициент прямой, содержащей высоту
– угловой коэффициент прямой, содержащей высоту 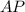 :
: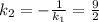
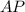 найдем по точке
найдем по точке 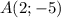 и угловому коэффициенту
и угловому коэффициенту 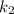 :
: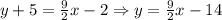
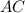 как уравнение с угловым коэффициентом:
как уравнение с угловым коэффициентом: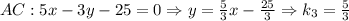
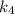 – угловой коэффициент прямой, содержащей высоту
– угловой коэффициент прямой, содержащей высоту 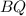 , то
, то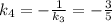
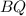 найдем по точке
найдем по точке 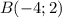 и угловому коэффициенту
и угловому коэффициенту 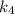 :
:
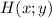 найдем, решив систему уравнений, задающих прямые
найдем, решив систему уравнений, задающих прямые 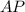 и
и 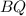 :
: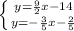
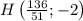
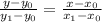
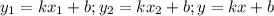
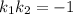 - признак перпендикулярности на плоскости
- признак перпендикулярности на плоскости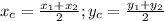
0 и 100
Пошаговое объяснение:
Если за столом есть лжец , тогда справа от него чудак или рыцарь.В такой ситуации оба они говорят правду, значит следующий после них снова лжец. Получается что лжецы и не лжецы чередуются. Т.е лжецов ровно половина.200/2=100
Если же лжецов за столом нет, то и рыцарей тоже нет( потому что справа от рыцаря должен быть лжец) и за столом одни чудаки. Значит количество лжецов 0