ответ: Два розвязка .
Якщо на одній прямій накреслить перше коло О₁ радіус якого дорівнює 22 см, то отримаємо відрізки перетинання кола з прямою АО₁ та О₁В. При цьму відрізки АО₁ = О₁В = r = 22 см.
На цій же прямій відкладем відрізок ВО₂, який дорівнює 42 см, та накреслим коло радіус якого дорівнює довжині відрізка ВО₂. Таким чином отримаємо другий відрізок О₂С.
При цьму відрізки ВО₂ = О₂С = r = 42 см.
Два кола торкаються, тоді відстань між центрами цих кіл дорівнює:
О₁В + ВО₂ = 22 + 42 =64 см
Відстань між центрами цих кіл О₁ та О₂ дорівнює 44 см.
Накреслим коло О₃ з радіусом 32 см. Проведемо діаметр цього кола, та отримаємо відрізки DO₃ та О₃N, при цьому DO₃ = О₃N = r = 22 см.
На відрізку О₃N відкладемо відрізок NО₄ довжиною 42 см.
Накреслим коло с центром О₄ радіусом довжини відрізка = 42 см.
На відрізку DN отримаємо відрізки МО₄ та О₄N при цьому МО₄ = О₄N = r = 42см.
Два кола торкаються, тоді відстань між центрами цих кіл дорівнює.
Так як відрізок О₃О₄ належить відрізку O₃N, тоді можемо знайти відрізок О₃О₄.
О₃М = О₃N - MO₄ - O₄N
O₃M = 22 - 42 - 42 = 22 cм
O₃O₄ = O₃M + MO₄
O₃O₄ = 22 + 42 = 64 см
Відстань між центрами цих кіл О₃ та О₄ дорівнює 20 см.
Пошаговое объяснение:
Пошаговое объяснение:
1. y=x²+8x+10
парабола ветвями вверх
критическая точка
y'=2x+8=2(х+4) 2(х+4) = 0 ⇒ x=-4; y= -6 точка (-4; -6)
она же вершина параболы
(-∞; -4) y'(x) < 0 функция убывает
(-4; *∞) y' (x) > 0 функция возрастает
точка (-4; -6) - точка минимума
нули функции
x²+8x+10=0
D= 24; x₁,₂= -4± √6 ⇒ x₁ ≈ -1.6 x₂ ≈ -6.5
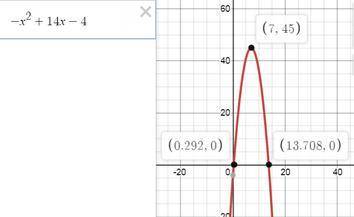
2. y=-x²+14x-4
парабола ветвями вниз
критическая точка
y'=-2x+14 -2х+14=0 ⇒ x=7; y= 45 точка (7; 45)
она же вершина параболы, она же максимум функции
нули функции
-x²+14x-4=0
D= 180; x₁,₂= -7± √45 ⇒ x₁ ≈ 0.3 x₂ ≈ 13.7
3. y=-x³/3+3x²/2-28x
критическая точка
y'=-x²+3x-28 -x²+3x-28=0 ⇒ D <0 корней нет, критических точек нет
-x²+3x-28 всегда меньше 0 - функция убывает на всей области определения
нули функции
-x³/3+3x²/2-28x = 0
x(-x²/3+3x/2-28) = 0 x₁ = 0 (квадратное уравнение корней не имеет)