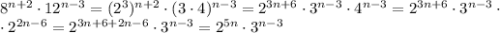
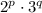Математика: 7(x+6)=4(5x+4) найдите корни уравнения

7(x+6)=4(5x+4) найдите корни уравнения

👇

Ответ:

Yanis2286

08.03.2020

7*x+7*6=4*(5x+4)
7x+7*6=4*(5x+4)
7x+42=4*(5x+4)
7x+42=4*5x+4*4
7x+42=20x+4*4
7x+42=20x+16
7x-20x=16-42
-13x=16-42
-13x=-26
x=-26/-13
x=2

4,4(99 оценок)

Открыть все ответы

Ответ:

sveta6729

08.03.2020

Сначала определим, как выглядят все делители заданного числа. Для этого стоит разложить его на простые множители:

$8^{n+2} \cdot 12^{n-3} = ( 2^{3} )^{n+2} \cdot (3\cdot4)^{n-3} = 2^{3n+6} \cdot 3^{n-3} \cdot 4^{n-3} = 2^{3n+6} \cdot 3^{n-3} \cdot \\ \cdot 2^{2n-6} = 2^{3n+6 + 2n-6} \cdot 3^{n-3} = 2^{5n} \cdot 3^{n-3}$

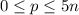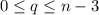
Из этого разложения заключаем, что все делители имеют вид: $2^{p} \cdot 3^{q}$ , где $0 \leq p \leq 5n$ , $0 \leq q \leq n-3$

По условию это число имеет 42 натуральных делителя.
1)Пусть сначала q = 0

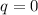, то есть, каждый из 42 делителей есть степень двойки. Очевидно, что эти делители располагаются лишь в порядке возрастания степеней двойки "без пропусков"(иначе получится число, имеющее более 42 делителей), поэтому 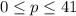$0 \leq p \leq 41$ (между 0 и 41 располагается ровно 42 натуральных числа). А чтобы всех таких делителей вида 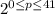$2^{0 \leq p \leq 41}$ было ровно столько, необходимо, чтобы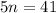
5n = 41

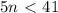Если $5n \ \textless \ 41$ ,то таких делителей меньше 42, если 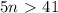$5n \ \textgreater \ 41$ , то больше.
Итак, 5n = 41

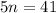, откуда 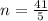$n = \frac{41}{5}$ - не натуральное число. Поэтому делаем вывод: среди делителей данного числа не могут содержаться только лишь степени двойки.

2)Повторим рассуждения для степеней тройки.
Пусть p = 0

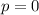для всех делителей. Тогда они имеют вид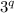 $3^{q}$
В силу рассуждений предыдущего пункта, n - 3 = 41

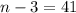, откуда

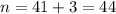- натуральное число. Этот случай вполне нас может устраивать, но здесь обязательна проверка - подстановка n в запись числа и прикидка количества делителей. Подставляя, имеем число: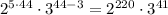
$2^{5 \cdot 44} \cdot 3^{44-3} = 2^{220} \cdot 3^{41}$
Но мы видим, что число имеет 220 делителей, только лишь являющихся степенями двойки, не говоря про остальные делители(то есть, их не 42 явно). Поэтому n = 44

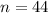условию задачи не удовлетворяет.

3)Пусть теперь имеем среди делителей и делители "смешанной" породы.

Как найти нам теперь n?
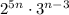Пусть у нас есть какое-либо число вида $2^{5n} \cdot 3^{n-3}$ . Какова структура делителей данного числа? Их три вида:
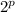а)Вида $2^{p}$ . Очевидно, что 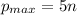$p_{max} = 5n$ , а потому всего их 5n+1

;
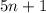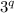б)Вида $3^{q}$ . Ясно, что 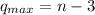$q_{max} = n-3$ , а всего их n-3+1 = n-2
Плюс ко всему замечаем, что два раза получается в делителе 1. Так что один лишний делитель я выбрасываю.
О чём это всё говорит? О том, что "чистых" делителей в точности
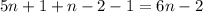5n+1 + n-2 - 1 = 6n - 2

(убираем 1 отсюда)

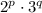в)Смешанные делители вида $2^{p} \cdot 3^{q}$ . Сколько их? Здесь уже практически чистая комбинаторика. Подсчитываем общее допустимое число делителей.
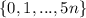На каждую из $\{0, 1, ..., 5n\}$ степеней числа 2(всего их 5n+1

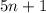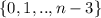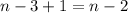, но 0 не включается, а потому только 5n) можно поставить одну из $\{0, 1, .., n-3\}$ степеней числа 3(всего их n-3+1 = n-2

, но 0 не включаем, а потому n-3). Соответственно, получаем 5n(n-3)

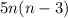их комбинаций.

Всего делителей 42, так что
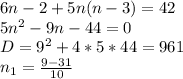$6n-2 + 5n(n-3) = 42 \\ 5 n^{2} -9n -44 = 0 \\ D = 9^{2} + 4 * 5 * 44 = 961 \\ n_{1} = \frac{9 - 31}{10}$ - не натуральное и даже не целое число.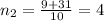
$n_{2} = \frac{9 + 31}{10} = 4$

Таким образом, n = 4

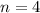. Произведём проверку:

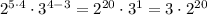$2^{5\cdot4} \cdot 3^{4-3} = 2^{20} \cdot 3^{1} = 3\cdot 2^{20}$ - действительно, число имеет 42 натуральных делителя(40 - отличных от 1 и самого числа, и 2 особых делителя - само число и 1).

4,4(89 оценок)

Ответ: