Павел Петрович, Александр Павлович, Николай Павлович, Александр Николаевич, Александр Александрович, Николай Александрович.
Пошаговое объяснение:
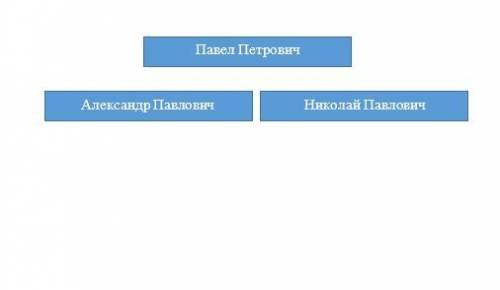
Павел Петрович не мог быть никому из них сыном или братом. У него одного только отчество Петрович. Значит он был первым. Тогда у него было два сына: Александр Павлович и Николай Павлович. См. рис.1
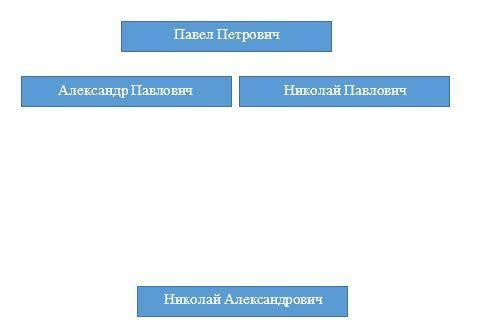
Последний был Николай. Николай Павлович, как выяснили, был или вторым, или третьим. Значит, последним был Николай Александрович. См. рис.2
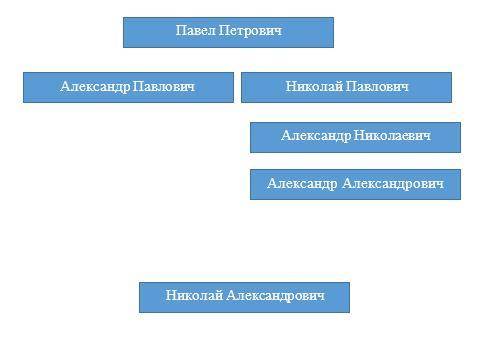
Осталось двое: Александр Александрович и Александр Николаевич. Если бы Александр Александрович был сыном Александр Павловича, то Александр Николаевич не мог бы быть его сыном. Значит, сын был у Николай Павловича. См. рис.3
Ну и поскольку сыновья следовали сразу за отцами, получаем окончательный порядок следования. См. рис.4

84+1=85
24×85=2040