По теореме синусов a/sin(π/3) = b/sin(β) (a - известная сторона ,sin(π/3) - известный угол ) ,подставляя численные значения ,получаем b = 20 * sin(β). Для того, чтобы b был максимальный ,нужно ,чтобы sin(β) был максимальным ,при этом β<120° (т.к. сумма углов в треугольнике должна быть равна 180°) .От 0 до 180° , максимальный sin достигается при β = 90°.Значит максимальная сторона будет достигнута в прямоугольном треугольнике и этой стороной будет гипотенуза. sin(π) =1 ,b = 20 * sin(β) =20
ответ : 20
1. AC = 12
2. BD = 2
3. DC= 4; AC =16; AB=4 \sqrt{12}
Пошаговое объяснение:
1. DE треугольника DBE находится по теореме Пифагора: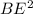 
= 
+ 
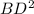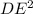, где DE=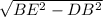 
Так как DE = средняя линия треугольника ABC (AD = DB) то AC = 2DE. Отсюда, AC= 12
2. AC находится по той же теореме Пифагора: AC =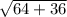
=10
BD = медиана треугольника ABC, так как она делит AC на равные отрезки, тогда
BD =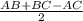
= (6+8-10)/2 =2
3. DC= 4 - показано на рисунке.
Так как угол DBC треугольника BDC равен 30 градусам, то гипотенуза этого треугольника будет равна 8, потому что катет, лежащий против угла в 30 градусов в прямоугольном треугольнике равен половине гипотенузы. Значит BC = 8.
Если угол DBC = 30 градусов, то смежный ему угол DBA= 60 градусов, так как угол ABC = 90 градусов. Теперь рассмотрим прямоугольный треугольник ADB. Если угол DBA = 60 градусов, то угол BAD = 30 градусов. Так как угол BAD =30 граудсов, то BC =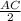 
. Получается, что AC = 16. Для нахождения AB применим теорему Пифагора: AB =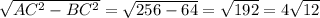
(8+2)*2=20 см периметр прямоуг
периметры равны
2) площади-конечно нет
Пл. квадрата = 5*5=25 кв. см
Пл. прям=8*2=16 кв.см