Получается что росло 16890 груш
скорее всего если вы пятом классе, вы решаете в столбик , поэтому некоторые решения , которые нельзя посчитать устно, я прикреплю в фото.
Задание 1
5,006
5,020
5,028
5,065
5,650
Задание 2
а) 54,36 • 0,1= 5,436
b) 93,5 • 1000= 93500
c) 42,5 • 7,2 = 306
d) 485,55 : 100 = 4,8555
e) 32,12 : 0,01 = 3212
f) 29,4 : 7,5 = 3,92
Задание 3
Пусть первый сосуд вмещает х+3,6 л , второй х л, поскольку вместе их вместимость 12,8 л,
составим уравнение:
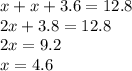
(л) — второй сосуд
4,6+ 3,6 = 8,2 (л)
ответ: 8,2 л — вместимость большего сосуда.
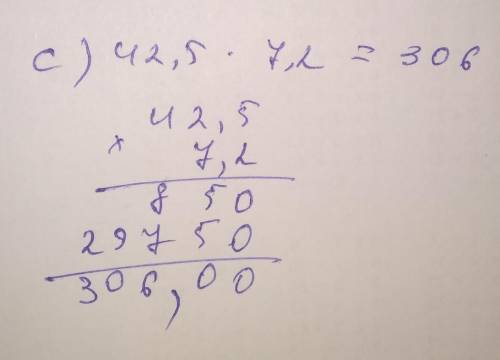
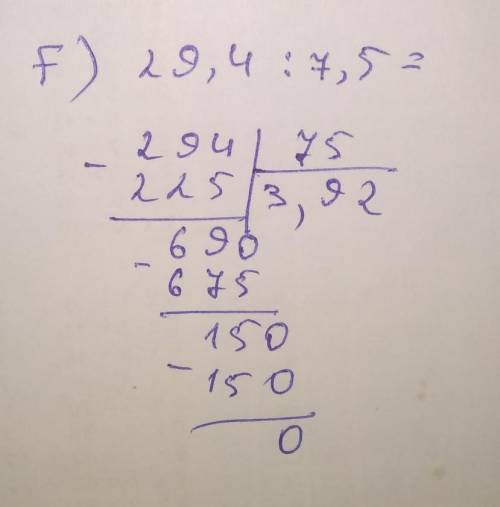
Допустим, вы освоили метод интервалов (если не освоили — рекомендую вернуться и прочитать) и научились решать неравенства вида P(x)>0P(x)>0, где P(x)P(x) — какой-нибудь многочлен или произведение многочленов.
Полагаю, что для вас не составит труда решить, например, вот такую дичь (кстати, попробуйте для разминки):
(2x2+3x+4)(4x+25)>0;x(2x2−3x−20)(x−1)≥0;(8x−x4)(x−5)6≤0.(2x2+3x+4)(4x+25)>0;x(2x2−3x−20)(x−1)≥0;(8x−x4)(x−5)6≤0.
Теперь немного усложним задачу и рассмотрим не многочлены, а так называемые рациональные дроби вида:
P(x)Q(x)>0P(x)Q(x)>0
где P(x)P(x) и Q(x)Q(x) — всё те же многочлены вида anxn+an−1xn−1+...+a0anxn+an−1xn−1+...+a0, либо произведение таких многочленов.
Это и будет рациональное неравенство. Принципиальным моментом является наличие переменной xx в знаменателе. Например, вот это — рациональные неравенства:
x−3x+7<0;(7x+1)(11x+2)13x−4≥
1) 563×30=16 890
Відповідь: 16 890
вроде так