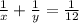. Половину работы каждый из них выполняет с той же производительностью, а значит время, затраченное на её выполнение равно 
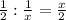и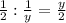 
для первого и второго штукатура соответственно. Мы знаем, что работая по очереди они затратили 25 часов. Таким образом получаем систему уравнений: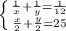
1) 4,2×(-0,3)=-1,26
2) -1,26÷0,9=-1,4
3) 5,6÷(-14)=-0,4
4) -0,4×3,7=-1,48
5) -1,4+1,48=0,08