Пошаговое объяснение:
Объем большого покрашенного куба:
V=8x8x8=512см³
Объем каждого кубика после распила:
V=1x1x1=1см³
Значит всего при распиле получилось 512 кубиков
Теперь находим остальное:
а. Три части могут быть окрашены только у углов изначального куба, таких кубиков получилось 8, по одному на каждый угол, 8/512 это 1/64 или 0.015625
б. Две части могут быть окрашены у тех частей, которые были ребрами изначального куба, не считая углы, у них три окрашенных части. У куба 12 ребер, каждое ребро содержит один ряд из 8 кубиков, но 2 (как угловые) мы исключаем, получается 6х12=72 кубика, 72/512 это 9/64 или 0.140625
в. Одна часть может быть окрашена у тех частей, которые были серединами сторон, находились между ребер куба, это сетка 6х6см, с каждой из 6 сторон куба, получается 6х6х6=216 кубиков, 216/512 это 27/64 или 0.421875
г. Неокрашенные части находились внутри, в теле куба, они составляют объем внутреннего куба со стороной 6х6см, т.к. весь внешний слой мы уже разобрали выше, получается 6х6х6=216 кубиков, 216/512 это 27/64 или 0.421875
Проверка: 8/512+72/512+216/512+216/512=512/512 - верно, все сходится
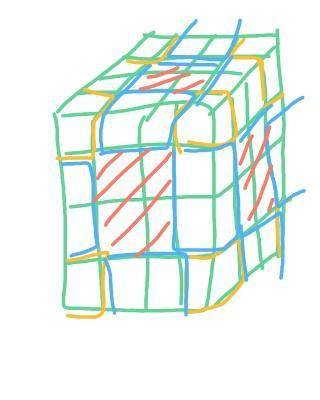
Для примера я нарисовал кубик 4х4см, на нем желтым выделены углы (случай А), синим ребра (случай Б) и красным серединки (случай В), остальное, то что не видно, это случай Г
Пошаговое объяснение:
Пусть скорость велосипедиста из А в В - х км /ч, тогда скорость из В в А x + 2 км/ч , а время, за которое велосипедист проехал путь из В в А 224 х ч, соответственно время, за которое велосипедист путь из А в В 224/x+2 +2 ч
Составим уравнение:
224/x + 2 + 2 = 224/x
224x + 2x² + 4x = 224x +448
2x² + 4x - 448 =0 | :2
x² + 2x - 224=0
D= 2²- 4* ( -224)= 4 + 896 = 900
√900 = 30
x1 = (-2 - 30)/2 = - 16 (не подходит по условию задачи, т.к скорость не может быть отрицательной
x2 = (-2 + 30)/2 = 14 км/ч скорость с А в В
14 + 2 = 16 км/ч скорость туриста на пути из В в А
х+7+6-4=х+9 воды станет
х-6-льда станет
х+9-(х-6)=х+9-х-6=3 т -на столько