1.60 умножить на 3=180(км) проехал за 3 часа;
2.50 умножить на 2=100(км) проехал за 2 часа;
3.180 + 100=280(км) всего проехал;
4.60 + 50+110(км в час) общая скорость;
5.3 + 2=5(час) всего времени;
6.110 : 5=22(км в час)
ответ:22 км в час средняя скорость автомобиля на всём пути
Відповідь:
1 та 2
Пояснення:
Розкладемо ліву частину нерівності на множники, розв'язавши відповідне квадратне рівняння:
-2x²+5x-2 = 0
2x²-5x+2 = 0
D = b²-4ac = (-5)²-4·2·2 = 25-16 = 9
x_1 = (-b+√D)/2a = (5+√9)/(2·2) = (5+3)/4 = 2
x_2 = (-b-√D)/2a = (5-√9)/(2·2) = (5-3)/4 = 0,5
Тоді -(2x²-5x+2) = -2(x-0,5)(x-2) = (2x-1)(2-x)
Тепер нерівність перетворена до такої: (2x-1)(2-x) ≥ 0
Розв'яжемо її методом інтервалів. Позначимо нулі функції в лівій частині нерівності (корені щойно розв'язаного рівняння) на числовій прямій та з'ясуємо знак цієї функції на кожному з проміжків, які утворяться (проставимо "+" або "-").
- + -
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(0,5)¯¯¯¯¯¯¯¯¯¯¯¯¯¯(2)¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Множиною розв'язків буде проміжок, на якому функція набуває невід'ємних значень. Тобто x ∈ [0,5; 2]. Йому належать лише два цілих числа: 1 та 2.
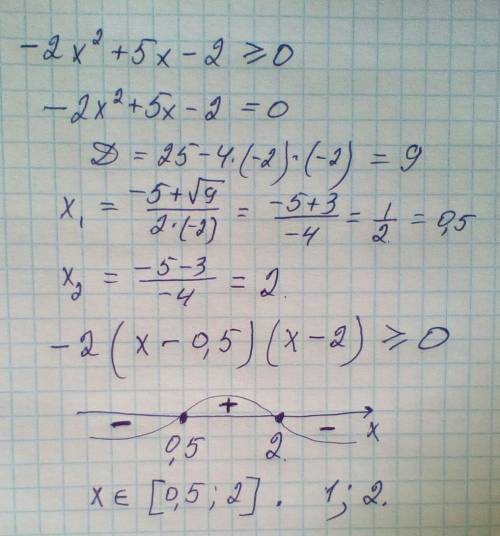
Пошаговое объяснение:
Узнаем скорость сближения:
1) 80 - 60 = 20 ( км/ч ) - скорость сближения.
Узнаем время пути:
2) 40 : 20 = 2 ( ч ) - время пути.
Обратная задача:
Условие:
Из посёлка A выехал легковой автомобиль со скоростью 80 км/ч, а из посёлка Б выехал грузовик со скоростью 60 км/ч. Через 2 часа после начала движения легковая машина догнала грузовик. Какое расстояние между посёлками?
Узнаем скорость сближения:
1) 80 - 60 = 20 ( км/ч ) - скорость сближения.
Узнаем расстояние между посёлками:
2) 20 * 2 = 40 ( км ) - расстояние между посёлками.
1. 2*50=100 км проехал со скоростью 50км/ч
2. 3*60=180 км проехал со скорость 60км/ч
3. (100+180):(2+3)=280:5=56 км/ч средняя скорость