№1; №2; №4
Пошаговое объяснение:
1. У каждого мальчика из класса Оли поровну одноклассников-мальчиков и одноклассниц-девочек.
Верно.
12 - 1 = 11 (м.) столько одноклассников-мальчиков у каждого мальчика
11 = 11 число одноклассников-мальчиков равно числу одноклассниц- девочек
2. У Оли в классе мальчиков не больше 12
Верно.
12 = 12, а не больше
3. У каждой девочки из класса Оли поровну одноклассников-мальчиков и одноклассниц-девочек.
Неверно.
11 - 1 = 10 (д.) столько одноклассниц у каждой девочки
10 < 11;
4. У Оли 22 одноклассника.
Верно.
11 + 12 = 23 (ш.) --- всего школьников в классе Оли.
23 - 1 = 22 (ш.) --- всего одноклассников у Оли
У дроби, где числитель и знаменатель меньше соответствующих в другой дроби, вид такой:
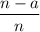
У другой дроби вид такой:
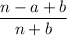
Вот теперь их сравним
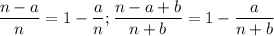
Для a, b и n имеется в виду, что это натуральные числа.
Получается, что фактически мы сравниваем
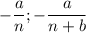
Если без минуса сравнивать их, то тогда дробь, где знаменатель больше, будет меньше (по аналогии делим пирог: на 3 части или на 7 частей, где на 7 частей, куски будут меньше).
А если с минусом, то тогда наоборот все, получаем, что
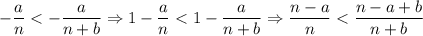
То есть больше будут дроби, где числитель со знаменателем больше.
В 1-ом случае у нас n=62, a=1, b=1 (вместо букв можно подставить эти числа и получить дроби из условия)
В 2-м случае у нас n=107, a=4, b=900
В 1-м случае получаем, что
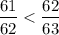
В 2-м случае получаем, что
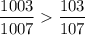
(99+9)/9=12