8 вариантов
Пошаговое объяснение:
выберем предмет, с которого оно начнется. Например, кепку, она же выше всех? Конечно же мы выберем красную кепку! Ставим от еще не выбранной кепки в начале выбора ветку - красную линию. (Но, чтобы не забыть, что была возможность выбора синей, и что к этой возможности надо вернуться, составив все варианты для красной кепки, сразу от начальной кепки рисуем и синюю линию).
Красная кепка + Красная футболка. Или Красная кепка + Синяя футболка. Т.е. от Красной кепки надо нарисовать две ветки - синюю и красную.
Идем по красной. Для шорт от красной футболки рисуем еще две ветки - красную и синюю. т.е. Если идти от кепки по ветке Красной кепки и Красной футболки, получим два варианта. Сокращенно ККК и ККС.
Веток от шорт нет, так как больше выбора , например, кроссовки двух цветов, в условии нет. Поэтому вернемся к ветке Синей футболки и нарисуем ветки для нее. Это, конечно, тоже Красные шорты и Синие шорты. Получаем варианты (идя от красной кепки!) КСК и КСС.
Аналогично рисуем ветки и для синей кепки - по две ветки (две возможности) для каждой вещи. Получаем еще 4 варианта: СКК, СКС, ССК и ССС.
Всего 8 вариантов.
Задача: Найдите коэффициент a, если парабола y = ax² проходит через точку a(-2;12).
Подставим координаты точки в уравнение параболы и выразим из него коэффициент a:
12 = (-2)²a
12 = 4a
a = 3
ответ: a = 3.
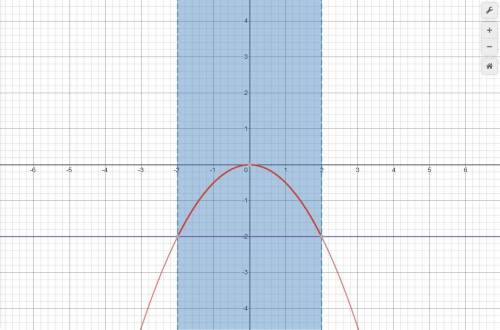
Задача: С графика функции y = -0.5x² решите неравенство -0.5x² > -2.
(прикреплено)
y = -0.5x² — красный графикy = -2 — фиолетовый графикответ: -2 < x < 2 или x ∈ (-2; 2).
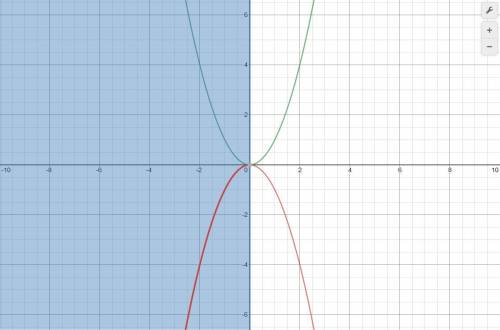
Задача: На одной координатной плоскости постройте графики функций y = x² и y = -x². Используя графики, выяснить, какая из этих функций возрастает на промежутке x ≤ 0.
(прикреплено)
y = x² — зеленый графикy = -x² — красный графикответ: На промежутке x ≤ 0 возрастает ф-ция y = -x².
Дано: y = x²/(x²-1),
ИССЛЕДОВАНИЕ.
1. Область определения: в знаменателе х²-1 = (х-1)*(х+1) ≠ 0.
D(y)= X≠ ±1 , X∈(-∞;1)∪(1;1)∪(1;+∞). Не допускаем деления на 0 в знаменателе.
2. Разрыв II-го рода при Х = ±1.
Вертикальные асимптоты - Х = -1 и Х = 1.
3. Наклонная асимптота: k = lim(+∞)Y(x)/x = 0 . b = 0 и
y(x) = 0 - горизонтальная асимптота.
4. Нули функции, пересечение с осью ОХ.
Y(x) =0. Нулей функции - нет.
Пересечение с осью ОУ : Y(0) = -1.
5. Интервалы знакопостоянства.
Отрицательна: Y(x)<0 - X∈(-1;1). Положительна: Y>0 - X∈(-∞;-1)∪(1;+∞;)
6. Проверка на чётность.
Функция чётная. Y(-x) = Y(x) ,
7. Поиск экстремумов по первой производной.
y'(x) = 2*x/(x²-1)- 2*x/(x²-1)² = -4x/(x²-1)² = 0.
x₁ = 0, x₂ = -1, x₃ = 1 - точки экстремумов.
8. Локальный максимум: y(0) = 0.
9. Интервалы монотонности.
Возрастает - X∈(-∞;-1)∪(-1;0). Убывает: X∈(0;1)∪(1;+∞).
10. Поиск перегибов по второй производной.
y"(x) = (12*x²+4)/(x-1)³ = 0
Точки перегиба нет, кроме разрывов при Х = ±1.
11. Вогнутая - "ложка"- X∈(-∞;-1)∪(1;+∞;), выпуклая - "горка" - X∈(1;1);
12. Область значений. E(y) - y∈(-∞;+∞).
13. График функции на рисунке в приложении.