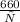 деталей, а второй рабочий -
деталей, а второй рабочий - 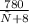 часов. Известно, что первый рабочий делает за час на 4 детали больше, чем второй. Исходя из этого, составляем уравнение:
часов. Известно, что первый рабочий делает за час на 4 детали больше, чем второй. Исходя из этого, составляем уравнение: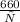 -
- 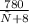 = 4 | ×x(x+8)
= 4 | ×x(x+8)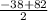 = 22
= 22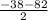 = -22
= -22Формула Эйлера для многогранников.
Пусть В — число вершин выпуклого многогранника, Р — число его ребер и Г — число граней. Тогда верно равенство В+Г=Р+2.
Октаэдр - многогранник с 8 гранями. (Грани- треугольники)У него 6 вершин и 12 ребер.
8+6=12+2. Формула Эйлера верна.
Додекаэдр - многогранник, состоящий из граней- пятиугольников.Этих граней 12.У него 30 ребер и 20 вершин.
20+12=30+2 Формула Эйлера верна.
Икосаэдр - многогранник, состоящий из 20 граней-треугольников.
У него также, как и у додекадра,
30 ребер и 20 вершин.
20+12=30+2 Формула Эйлера верна.
пусть х деталей в час делает первый рабочий, тогда второй (х-4)
360/x - время первого
520/(x-4) - время второго
520/(x-4)-360/x=8
520x-360(x-4)=8x(x-4)
520x-360x+360*4=8x(x-4)
160x+180*8=8x(x-4)
20x+180=x2 -4x
x2 -24x-180=0
x=30 x=-6
ответ:30