Дано уравнение √(2x+4) = 1 - 2x.
ОДЗ: 2x + 4 ≥ 0, х ≥ -2,
1 - 2x ≥ 0, х ≤ 1/2.
Вывод: обе части его - положительны.
Левая часть - возрастающая функция, правая - убывающая.
Значит, есть одна точка пересечения, в которой справедливо равенство (если оно существует).
Возведём его в квадрат: 2x + 4 = 1 - 4x + 4x².
4x² - 6x - 3 = 0. Д = 36 + 4*4*3 = 84. √84 = 2√21.
х1 = (6 + 2√21)/8 = (3 + √21)/4 ≈ 1,89564. По ОДЗ не принимаем.
х2 = (6 - 2√21)/8 = (3 - √21)/4 ≈ -0,39564.
ответ: корень один и равен х = (3 - √21)/4 ≈ -0,39564.
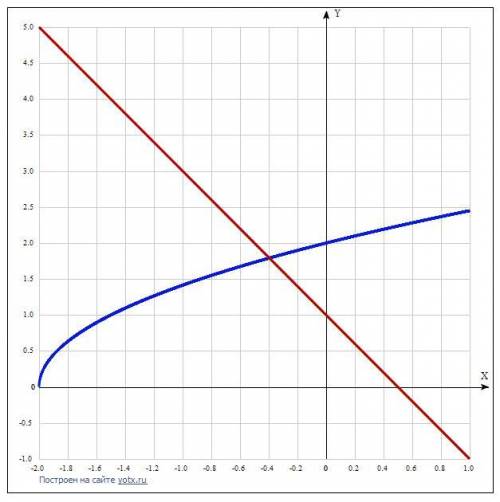
ответ можно подтвердить графически: ведь корень - это точка пересечения двух графиков у = √(2x+4) и у = 1 - 2x.
1.
2,8 * (-3,9) - 76,15 : 15,23 = -15,92
1) 2,8 * (-3,9) = -10,92
2) 76,15 : 15,23 = 5
3) -10,92 - 5 = -15,92
ответ: -15,92
2.
34,68 : (7,11 + 1,56) + 46 : (2,45 - 1,65) = 61,5
1) 7,11 + 1,56 = 8,67
2) 34,68 : 8,67 = 4
3) 2,45 - 1,65 = 0,8
4) 46 : 0,8 = 57,5
5) 4 + 57,5 = 61,5
ответ: 61,5
3.
(0,62 + 0,56 - 2,29) * (8,44 - 5,34) = -3,441
1) 0,62 + 0,56 = 1,18
2) 1,18 - 2,29 = -1,11
3) 8,44 - 5,34 = 3,1
4) -1,11 * 3,1 = -3,441
ответ: -3,441
4.
62,93 + (12,5 - 7,6 + 3,21) : 0,1 = 144,03
1) 12,5 - 7,6 = 4,9
2) 4,9 + 3,21 = 8,11
3) 8,11 : 0,1 = 81,1
4) 62,93 + 81,1 = 144,03
ответ: 144,03
y'=2cosx-2sin2x
2cosx-2sin2x =0, 2cosx(1-2sinx)=0,
2cosx=0,
1-2sinx=0,
x=pi/2+pi*n, x=pi/6+2pi*n
2. проверим входят ли корни в заданный отрезок
входят корени: pi/2, 3pi/2, pi/6, 5pi/6
3. находим значения выражений:
y(0)=0+1=1
y(2pi)=0+1=1
y(pi/2)=2-1=1
y(3pi/2)=-2-1=-3
y(pi/6)=1+1/2=3/2
y(5pi/6)=1+1/2=3/2
из полученных ответов находишь самый наименьший и наибольший
наим=-3
наиб=3/2