1) 706 2712 + 167583 = 7230295.
2) (47 820 + 125 170) : 5 = 34 598.
1. 47 820 + 125 170 = 172 990.
2. 172 990 : 5 = 34 598.
3) 3 731 542 + 900 349 - 15 370 = 4 616 521.
1. 3 731 542 + 900 349 = 4 631 891.
2. 4 631 891 - 15 370 = 4 616 521.
4) 4 • (2 398 + 12 290) : 2 = 29 376.
1. 2 398 + 12 290 = 14 688.
2. 14 688 • 4 = 58 752.
3. 58 752 : 2 = 29 376.
5) 6 • (12 468 - 9 398) + 37 852 = 56 272.
1. 12 468 - 9 398 = 3 070.
2. 3 070 • 6 = 18 420.
3. 18 420 + 37 852 = 56 272.
6) 1 000 000 - 201 411 • 3 = 395 767.
1. 201 411 • 3 = 604 233.
2. 1 000 000 - 604 233 = 395 767.
1136 см
Пошаговое объяснение:
Если куб, со стороной А = 24 разрезать на кубики со стороной а = 2, то возможны следующие варианты окраса малых кубиков:
- неокрашенные кубики (изнутри куба)
- с одной окрашенной стороной (с граней большого куба)
- с двумя окрашенными сторонами (с ребер большого куба)
- с тремя окрашенными сторонами (с вершин большого куба)
У куба 6 граней. А значит всего окрашенных граней у малых кубиков будет:
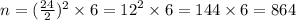
Вершин 8, значит, кубиков с 3мя окрашенными гранями тоже 8, окрашенных граней
8•3 = 24
Ребер 12, значит "двугранных" кубиков (за вычетом 8ми "трехгранных") будет:
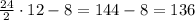
Окрашенных граней соеди них соответственно
136•2 = 272
Количество одногранных кубиков можно найти если вычесть из общего числа граней все "ненужные"
864 - 24 - 272 = 864 - 296 = 568 граней
Столько же и одногранных кубиков. А значит ряд, построенный из них будет размером:
568•2 = 1136 см
sin2x=√3cosx
2sinxcosx-√3cosx=0
cosx(2sinx-√3)=0
Произведение равно нулю, когда один из множителей равен нулю.
1) cosx=0
x=pi/2+pi*k, где k∈Z
2) 2sinx-√3=0
sinx=√3/2
x=pi/3+2*pi*n
x=2pi/3+2*pi*m, где m,n∈Z
б) Отбор корней:
k=0 x=pi/2 < pi не подходит
k=1 x=3pi/2 > pi подходит
k=2 x=5pi/2 =5pi/2 подходит
k=3 x=7pi/2 >5pi/2 не подходит
n=0 x=pi/3 < pi не подходит
n=1 x=7pi/3 подходит
n=2 x=13pi/3 >5pi/2 не подходит
m=0 x=2pi/3 < pi не подходит
m=1 x=8pi/3 >5pi/2 не подходит
ответ в б: 3pi/2; 7pi/3; 5pi/2