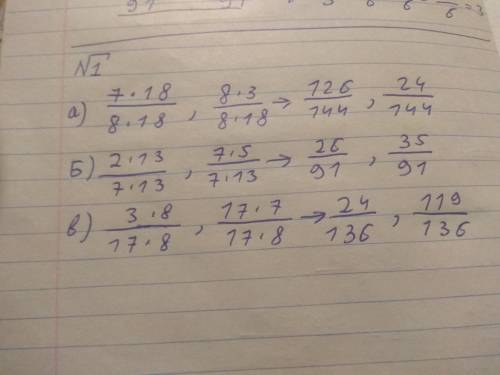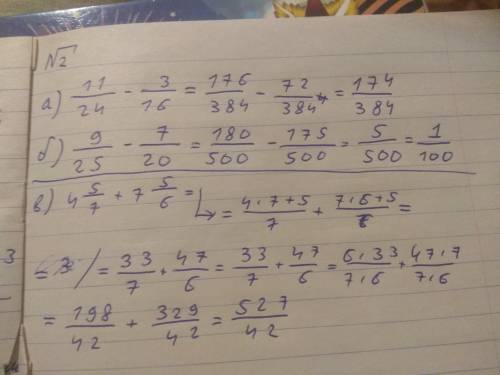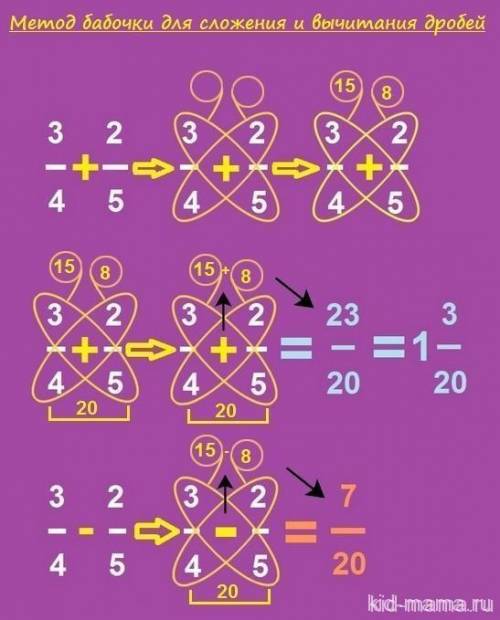ответ в приложении.
Пошаговое объяснение:
1) Рассмотрим случай, когда у уравнения будет один корень. В этом случае b=3, подставляем в исходное уравнение, получаем, что корнем является 6, но это посторонний корень, значит, корней нет.
2) Рассмотрим случай, когда у уравнения нет корней, то есть дискриминант меньше нуля. Таких значений нет.
3) Рассматривать случай, когда дискриминант больше 0 не имеет смысла, потому что у нас всегда будет два или один (в том случае, когда один из корней посторонний) корней.
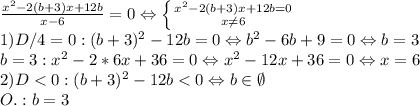
Пошаговое объяснение:
Задание 1
Мы приходим к общему знаменателю с метода "бабочка" : Суть «метода бабочки» заключается в том, чтобы прийти к общему знаменателю дробей нужно умножить числитель первой дроби на знаменатель второй, а затем числитель второй на знаменатель первой , и знаменатель второй на знаменатель первой .
Задание 2
Смысл тот же , только теперь сложение . Используем метод бабочки и складываем ( Суть «метода бабочки» заключается в том, что при сложении дробей нужно умножить числитель первой дроби на знаменатель второй, а затем числитель второй на знаменатель первой. Сумма двух получившихся чисел будет числителем дроби в ответе, а ее знаменателем — результат умножения знаменателей складываемых дробей).