(x - (-2))-(8·(-2)-(-14)·(-9)) - (y - 3)(3·(-2)-(-14)·1) + (z - 5)(3·(-9)-(-8)·1) = 0
(-110)(x - (-2)) + (-8)(y - 3) + (-19)(z - 5) = 0
- 110x - 8y - 19z - 101 = 0.
Если умножим на -1, то получим уравнение плоскости:
110 · x + 8 · y + 19 · z + 101 = 0 .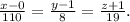
Направляющий вектор прямой имеет вид:s = 1; -6; -8
Вектор нормали плоскости имеет вид:q = 110; 8; 19
Угол между прямой и плоскостью:
С момента отправления до возвращения у одних поездов проходит 180 минут, у других - 120. Наименьшее общее кратное 180 и 120 равно 360 .
Разделим маршрут на 360 частей. Тогда поезда, идущие в одном направлении, будут следовать со скоростью 2 условные единицы в минуту, а интервал между ними будет составлять 30 условных единиц. Поезда, идущие в другом направлении, будут следовать со скоростью 3 условные единицы в минуту, а интервал между ними будет равен 45 условным единицам. В момент отправления восточного поезда расстояние между ним и первым встречным поездом составляет 45 условных единиц. Восточный поезд проходит 2/5 этого расстояния, встречный - остальные 3/5, после чего они встречаются в 18 условных единицах от станции отправления. Все последующие поезда восточный поезд встречает на расстоянии так же 18 условных единиц от места предыдущей встречи. В момент отправления западного поезда первый встречный поезд находится от него на расстоянии 30 условных единиц. Западный поезд проходит 3/5 этого расстояния, встречный - остальные 2/5, после чего они встречаются на расстоянии 18 условных единиц от станции отправления. Каждая последующая встреча западного поезда с восточными происходит на расстоянии 18 условных единиц от места предыдущей встречи.
Расставим вдоль всего маршрута 19 столбов, весь маршрут разделился на 20 частей по 18 условных единиц. Тогда поезда будут встречаться у каждого столба. Каждый 1 путешественник, вернувшись на станцию отправления, проедет мимо 19 столбов и встретит 19 поездов. Каждый 2 путешественник, едущий на восток, будет считать поезда после того, как он проедет 2/5 всего пути, то есть доедет до 8 столба. Значит он успевает сосчитать 12 поездов. Его конкурент сосчитает 8. Встреча их поездов происходит в конце 2/5 от 3 часов, или 3/5 от 2 часов, то есть спустя 72 минуты после отправления.