ответ: 8√3 см²
Пошаговое объяснение:
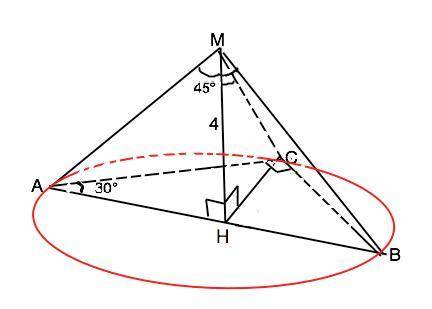
Обозначим пирамиду МАВС. Высота МН пирамиды перпендикулярна основанию и образует с боковыми ребрами углы 45°, следовательно, второй острый угол тоже 45°, боковые ребра - гипотенузы равных прямоугольных равнобедренных треугольников с общим катетом - высотой пирамиды, а их проекции равны радиусу описанной около основания окружности. Вершина пирамиды проецируется в центр этой окружности, – середину гипотенузы основания. АН=СН=ВН=МН=4 см, АВ=2•4=8 см. Катет АС=АВ•cos∠CAB=8•√3/2=4√3. Одна из формул площади треугольника S=0,5•a•b•sinα. ⇒ S(ABC)=0,5•0,AB•AC•sin30°=0,5•8•4√3•1/2=8√3 см²
ответ: 8√3 см²
Пошаговое объяснение:
Обозначим пирамиду МАВС. Высота МН пирамиды перпендикулярна основанию и образует с боковыми ребрами углы 45°, следовательно, второй острый угол тоже 45°, боковые ребра - гипотенузы равных прямоугольных равнобедренных треугольников с общим катетом - высотой пирамиды, а их проекции равны радиусу описанной около основания окружности. Вершина пирамиды проецируется в центр этой окружности, – середину гипотенузы основания. АН=СН=ВН=МН=4 см, АВ=2•4=8 см. Катет АС=АВ•cos∠CAB=8•√3/2=4√3. Одна из формул площади треугольника S=0,5•a•b•sinα. ⇒ S(ABC)=0,5•0,AB•AC•sin30°=0,5•8•4√3•1/2=8√3 см²

а) 7 * 3 + 8 = 21 + 8 = 29
б) 27 : 9 - 1 = 3 - 1 = 2
в) 3 + 15 : 5 = 3 + 3 = 6
г) 10 - 3 * 3 = 10 - 9 = 1
д) (29 + 9) - 15 = 38 - 15 = 23
е) 36 + (92 - 12) = 36 + 80 = 116
Задача.
на 1 ал. - 15 ск.
на 2 ал. - 22 ск.
унесли - 6 ск.
осталось - ? ск.
1) 15 + 22 = 37 скамеек - было всего
2) 37 - 6 = 31 скамейка - осталась
Выражением:
(15 + 22) - 6 = 31
ответ: 31 скамейка.