1,5 км/ч - скорость течения реки.
Пошаговое объяснение:
Пусть скорость лодки равна x км/ч, а скорость течения - у км/ч
Составляем уравнение для случая, когда лодка плыла по течению реки:
(x + y) * 3 = 69
Составляем уравнение для случая, когда лодка плыла против течения реки:
(х - у) * 4 = 80
Решаем систему уравнения:
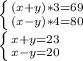
Выражаем из первого уравнения y и подставляем во второе уравнение:
y = 23 - x
--> x - (23 - x) = 20
Раскрываем скобки:
x - 23 + x = 20 --> 2x = 43 --> x=21,5 км/ч скорость лодки
Нам нужно найти скорость течения реки:
Подставляем х в любое из уравнений:
x + y = 23 --> 21,5 + y = 23 --> y = 23 - 21,5 = 1,5 км/ч - скорость течения реки.
75°
Пошаговое объяснение:
Задание
Найдите больший острый угол прямоугольного треугольника, если высота, проведенная к гипотенузе, в 4 раза меньше гипотенузы.
Решение
Теорема: около любого прямоугольного треугольника можно описать окружность, в которой гипотенуза прямоугольного треугольника является диаметром этой окружности, а медиана, проведённая из вершины прямого угла к гипотенузе, - её радиусом.
1) Обозначим исходный треугольник АВС (угол С - прямой, АВ - гипотенуза) и выполним вс построения:
- проведём из вершины прямого угла С медиану СМ к гипотенузе АВ;
- из того же угла С проведём высоту СН к гипотенузе АВ.
Так как около любого прямоугольного треугольника можно описать окружность, в котором гипотенуза является диаметром, то точка М является центром этой окружности, а медиана СМ и отрезки АМ и МВ гипотенузы АВ - её радиусами, равными половине диаметра, то есть половине гипотенузы АВ:
СМ = АМ = МВ = R = 1/2 АВ.
2) Согласно условию задачи, СН = 1/4 АВ, а это значит, что СН равен:
СН = 1/2 СМ, так как СМ = 1/ АВ.
Из этого следует, что в прямоугольном треугольнике СМН (угол Н - прямой) катет СН равен половине гипотенузы СМ, то есть лежит против угла М, равного 30°.
Следовательно, в равнобедренном треугольнике СМВ (СМ=МВ=R):
∠С = ∠В = (180 - 30) : 2 = 75°.
3) Так как ∠В является также и углом треугольника АВС, то из этого следует, что он является большим острым углом и равен 75°.
ответ: 75°.