Рассмотрим число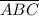 
.
Поскольку по условию средняя цифра должна быть больше суммы крайних цифр, то выберем в качестве В максимально возможную цифру, то есть 9.
Далее выгодно выбрать в качестве А и С наименьшие числа. В последовательных числах А меняется реже, поэтому сначала выберем А. В качестве А возьмем минимально возможную цифру - цифру 1.
Теперь в качестве С возьмем минимально возможную цифру - цифру 0. Получим число 190, для которого выполняется поставленное условие. Рассматривая следующие числа, получим, что это же условие выполняется для чисел 191, 192, ..., 197, но уже не выполняется для числа 198. Итого: 8 чисел - от 190 до 197 включительно.
Если увеличить А, то даже при минимальном значении С сумма А+С будет больше, чем в уже рассмотренном случае, а значит такой же длинной цепочки чисел получить не удастся.
ответ: 8
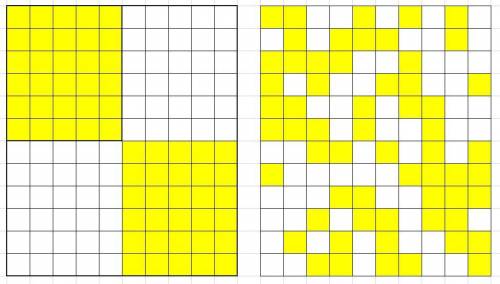
Рассмотрим наименьший такой прямоугольник. Это прямоугольник из 6 строк и 5 столбцов, в котором все клетки закрашены. Площадь его равна 30.
Если мы захотим добавить еще одну строку, то в ней также надо будет закрасить 5 клеток, но тогда во всех столбцах уже окажется закрашенными более 6 клеток. Значит, нам придется добавить еще 5 столбцов, в каждом из которых мы будем закрашивать клетки этой строки. Мало того, нам придется добавить еще 5 строк, чтобы выполнить условие о том, что во всех столбцах ровно 6 закрашенных клеток, а значит докрасить клетки, соответствующие столбцам из ранее добавленной строки. В результате число строк и число столбцов удвоилось, а площадь увеличилась в 4 раза и стала равной 120. Закрашенные клетки впоследствии можно менять местами, придерживаясь ограничений на них, но от этого размеры прямоугольника не изменятся.
Аналогично, исходная площадь 30 может увеличиться в 9, 16, 25 и так далее раз.
В общем виде возможная площадь выражается формулой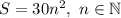 
. Из вариантов ответов подходит лишь число 120, которое как раз и получилось при рассуждениях.
ответ: 120
2(х+1) - 3(х+2)=6
2х+2-3х-6=6
-х=6+6-2
-х=10
х=-10
ответ: -10