ответ:
правило обращения периодической десятичной дроби в обыкновенную: чтобы периодическую десятичную дробь обратить в обыкновенную, надо из числа, стоящего до второго периода, вычесть число, стоящее до первого периода, и сделать эту разность числителем, а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде и после девятки дописать столько нулей, сколько цифр между запятой и первым периодом.
1.24-0=24 числитель
2.99= знаменатель
0,(24)=24/99=8/33
1. 3113-311=2802 -числитель
2. 900= знаменатель
3,11(3)=2802/900=1401/450
пошаговое объяснение:
Пошаговое объяснение:
Введем замену 
; 
.
Уравнение примет вид
Далее заметим, что для любого 
верно 
. То есть верхнее ограничение 
выполняется автоматически. Значит, полученная задача равносильна задаче о решении уравнения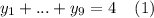 
в целых неотрицательных числах.
А для такой задачи применим метод шаров и перегородок: количество решений уравнения (1) совпадает с количеством размещений 4 неразличимых шаров в 9 ящиках [или, что то же самое, с количеством разделения ряда из 4 шаров 8 перегородками].
Искомое количество вариантов
Pквадрата=4*а, где a-сторона квадрата
Pтреугольника=3*а, где а-сторона треугольника
Подставляем известное значение стороны квадрата в формулу:
P=4*3
P=12 см
Из условий известно, что периметры двух фигур равны, подставляем известное теперь нам значение периметра в формулу периметра треугольника:
12=3*а
а=12:3
а=4 см
ответ: сторона треугольника равна 4 см.