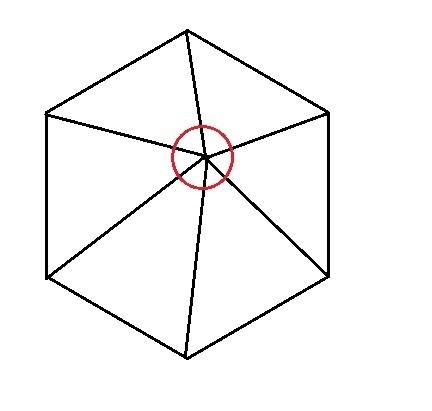
У нас есть правильный многоугольник. Поставим внутрь его точку, и проведем от этой точки отрезки ко всем углам многоугольника.
В итоге многоугольник разделится на треугольники.
Смотрим рисунок, на нем правильный 6-угольник.
Треугольников всегда будет столько же, как углов у многоугольника.
Сумма углов в каждом треугольнике равна 180°.
Сумма уголов во всех n треугольниках равна (180*n)°.
Сумма углов вокруг начальной точки (красная окружность) равна 360°.
Сумма углов многоугольника равна (180*n - 360)° = 180(n - 2)°
Так как многоугольник правильный, то все углы одинаковые.
Каждый угол равен 180(n - 2)/n. По условию он равен 108°.
180(n - 2)/n = 108
180(n - 2) = 108n
180n - 360 = 108n
180n - 108n = 360
n = 360/(180 - 108) = 360/72 = 5
Расчет сведен в таблицу.
Вероятность выбора случайного студента определим по их количеству на факультете - р1
р1э = 12/24 = 0,50 и р1ю = р1н = 6/24 =0,25.
Проверяем - сумма - р1 = 1,0 - правильно.
Вероятность сдачи экзамена - р2 - дана.
р2э = 0,6 и р2ю = 0,76 и р2н = 0,8.
Вероятность события Р = И любой И сдаст - равна сумме произведений вероятностей.
Р = р1э* р2э + р1ю*р2ю + р1н*р2н = 0,30+0,19+0,20 = 0,69.
Сдадут экзамен - 69% и провалят - 31%.
А теперь по формуле Байеса определим вероятность специальности для каждой группы
Для экономистов - 0,3/0,69 = 0,435
юристов - 0,19/0,69 = 0,275
налоговиков - ,20/0,69 = 0,29 = 29% - ОТВЕТ
Дополнительно - у налоговиков наименьшая вероятность провалить экзамен = 0,05/0,31 = 0,161 = 16,1%.